Chapitre 4 : Modélisation des capacités logiques

Nous présentons ici notre modélisation des connaissances déclaratives, représentées sous forme logique. Nous ne nous intéressons pas dans ce chapitre aux points concernant le couplage avec notre modélisation procédurale, qui seront présentés au chapitre 6.

Nous introduisons d’abord les travaux (menés à partir de l’étude de conversations spontanées) ayant débouché sur l’élaboration de notre modélisation logique. Trois modalités logiques apparaissent lors de cette étude (paradoxale, improbable et désirable/indésirable). Nous proposons alors une modélisation de ces trois modalités, ainsi que des mécanismes de calcul de réplique possibles. Nous indiquons ensuite les lieux où l’apprentissage est possible dans notre modélisation. Nous terminons ce chapitre par une synthèse de notre modélisation.

4.1 Etudes des conversations spontanées

Nous présentons ici les résultats obtenus lors de l’étude de conversations spontanées réelles menée par Jean-Louis Dessalles. Cette étude est en effet à la base de la représentation des connaissances logiques. C’est à partir de cette représentation qu’est construite notre modélisation des capacités logiques des sujets humains.

Nous ne proposons qu’un résumé suffisant pour la compréhension de la suite du chapitre : les justifications des points avancés ne sont donc pas proposées. Le lecteur intéressé pourra se reporter à [DES 93].

Le point essentiel de ce travail est que, contrairement à l’intuition, les interlocuteurs des conversations spontanées respectent des contraintes logiques fortes. Si ces contraintes sont violées, on observe de la part des autres interlocuteurs des réactions d’incompréhension ou de rejet, parfois teintées d’agressivité. Les autres résultats peuvent se résumer ainsi :

• Il n’existe que trois manières d’introduire un sujet nouveau. Nous dénommerons ces trois manières ‘modalités’ dans la suite de ce travail.

• Toute réplique doit avoir un effet logique sur la connaissance supposée de son interlocuteur.

• Le nombre et le type des répliques possibles à tout instant d’une conversation sont eux aussi limités en fonction de la modalité de la première réplique de cette conversation.

Un point de vue courant sur les conversations consiste à considérer celles-ci comme des coopérations entre les interlocuteurs. L’étude de Dessalles montre que les répliques successives d’une conversation ont plutôt pour rôle de détruire les répliques précédentes. Nous noterons cependant que cela ne remet pas nécessairement en cause le caractère coopératif des conversations, si l’on considère que la première réplique d’une conversation consiste en l’introduction d’une situation problématique. La destruction de la validité de la première réplique peut alors être vue par le premier locuteur comme une résolution de son problème.

Nous allons maintenant définir ce que nous entendons dans ce chapitre par conversation. Il s’agit pour nous d’un échange verbal entre interlocuteurs :

• ayant un même statut social.

• décontractés.

• se connaissant bien.

• se rencontrant fréquemment.

• n’étant pas engagés dans un dialogue finalisé (task-oriented).

• étant (momentanément) sérieux.

Cela exclut notamment du champ de l’étude les interactions de type enseignement, qu’il s’agisse de cours magistraux ou d’interactions moins formelles (petite classe, TD, …), les réunions de travail (brainstorming) et les communications unidirectionnelles (émission radio ou TV, discours, …).

H.P. Grice, dans ‘Logic and Conversation’ [GRI 75], indique un certain nombre de règles, ou ‘maximes’, que les interlocuteurs doivent usuellement respecter. L’une d’entre elle peut se formuler : ‘soyez pertinent’. L’objectif principal de l’étude des conversations de J.L. Dessalles est de définir les aspects logiques du concept de pertinence, et d’explorer toutes les manières d’être logiquement pertinent. Nous sommes maintenant en mesure d’aborder la présentation des résultats obtenus lors de cette étude, que nous appellerons ‘principes de pertinence conversationnelle’ :

• Premier principe : la première réplique d’une conversation doit toujours introduire une problématique.

• Second principe : les répliques suivantes d’une conversation doivent toutes avoir pour objet de détruire soit la validité de la problématique, soit la validité des arguments opposés à cette problématique.

Ces principes ne doivent pas être confondus avec le ‘principe de pertinence’ que Sperber et Wilson introduisent dans [SPE 89], p. 237, qui indique que ‘Tout acte de communication ostensive communique la présomption de sa propre pertinence optimale’. La pertinence est ici définie par la combinaison du coût cognitif de traitement d’une réplique et par l’effet contextuel que cette réplique produit. Le principe de pertinence de Sperber et Wilson est la garantie que fournit le locuteur à son auditeur sur le fait que :

a) L’effet de la réplique dépasse son coût cognitif

b) La réplique est telle que le coût cognitif pour parvenir à l’effet est le minimum possible.

Nous ne nous intéressons pas ici aux notions de coûts et d’effets cognitifs. Les travaux présentés ici ne vont donc ni dans le sens ni à l’encontre des travaux de Sperber et Wilson.

Nous avons toutefois un point de désaccord sur ce qu’est une réplique pertinente. Sperber et Wilson considèrent qu’une réplique ayant un effet contextuel sera nécessairement pertinente, alors que nous considérons qu’une réplique pertinente sera une réplique qui modifie ou introduit une problématique. Ces deux théories prédisent une réaction différente à des changements de sujet. Un changement de sujet ne sera jamais pertinent pour Sperber et Wilson, puisqu’il n’a aucun effet contextuel, alors qu’il pourra l’être pour nous.

Nous ne rejetons pas la théorie de Sperber et Wilson, mais nous considérons que les contraintes que pose cette théorie ne suffisent pas à expliquer une conversation réussie. En d’autres termes, les contraintes posées par Sperber et Wilson sont peut-être nécessaires, mais elles ne sont pas suffisantes. Nous noterons également que la théorie de Sperber et Wilson s’applique à tout acte de communication ostensive (i.e. tout acte où le locuteur rend manifeste à son interlocuteur son intention de lui communiquer quelque chose), alors que notre théorie s’applique en premier lieu aux conversations. Le cadre de notre étude étant ici plus restreint, il n’est pas surprenant de pouvoir exhiber des contraintes plus fortes.

4.1.1 Une première réplique sous la forme d’une problématique

La première réplique d’une conversation consiste toujours en l’expression d’un problème. Ce problème est introduit selon un des trois modes suivants, que nous nommerons ‘modalité’ :

• ‘Paradoxal’. Le premier interlocuteur exprime son étonnement devant une situation qu’il a rencontrée et qu’il juge logiquement impossible.

• ‘Improbable’. Le premier interlocuteur exprime sa surprise devant une situation qu’il a rencontrée et qu’il juge a priori improbable ou très peu fréquente.

• ‘(In)désirable’. Le premier interlocuteur présente une situation rencontrée qu’il considère comme (dés)agréable.

Nous appellerons situation problématique, ou plus simplement ‘problématique’, une situation pouvant s’exprimer selon l’une des trois modalités précédentes (paradoxale, improbable, ou désirable/indésirable).

La première réplique d’une conversation sera problématique en fonction d’un contexte logique. Si ce contexte n’apparaît pas clair aux autres interlocuteurs, il peut s’ensuivre une phase de discussion dont la finalité est d’instancier ce contexte. L’objectif de cette mise en contexte est de préciser pour les autres interlocuteurs en quoi la situation est problématique. Une fois la mise en contexte effectuée, la conversation entre dans sa deuxième phase. On notera que la mise en contexte peut échouer, les autres interlocuteurs comprenant une problématique différente de celle amenée par le premier : on se trouve en situation de quiproquo.

Une fois le contexte établi, les répliques suivantes sont cantonnées :

• Au co-étonnement (modalité improbable), à la co-incompréhension (modalité paradoxale), au co-réjouissement (modalité désirable) et à la co-lamentation (modalité indésirable). Dans tous ces cas, les autres locuteurs accusent réception de la problématique et ne voient pas de moyen pour y remédier. La conversation s’arrête.

• A l’invalidation logique, possible pour toutes les modalités, et qui peut prendre deux formes.

• A la banalisation, possible pour les modalités improbable et (in)désirable.

• A l’antagonisation, possible pour la seule modalité (in)désirable.

L’invalidation logique, la banalisation et l’antagonisation sont présentées plus en détail dans le paragraphe 4.1.2. Les réactions de compréhension/abandon ne seront pas présentées plus avant, compte tenu de leur manque d’intérêt pour la suite de nos travaux.

Précisons que le terme ‘logique’ n’est pas à prendre ici au sens de calcul ou maintien de valeurs de vérité mais plutôt comme moyen de représenter la signification et la pertinence de chaque réplique. Ainsi, le modèle n’interdit pas des répliques du type : ‘Je sais qu’il faut que je m’arrête et pourtant je ne le ferais pas’ (en parlant de tabagisme) qui peuvent paraître paradoxales d’un strict point de vue logique mais qui ne reflètent qu’une antagonisation.

4.1.1.1. La modalité paradoxale

La première façon de commencer une conversation est de présenter une situation qui paraît impossible au premier locuteur et qu’il a pourtant rencontrée. Il s’agit de la modalité paradoxale. Un exemple d’une telle première réplique est [DES 93] (p. 24) :

contexte : A vient de traverser en voiture un village du sud-ouest de la France. A l’entrée, un panneau mentionnait un jumelage avec une ville d’Alsace. A s’attendait à ce que deux villes jumelées appartiennent à deux pays différents.

A1 - Tout à l’heure, j’ai vu un village jumelé avec une ville d’Alsace !

A indique donc qu’il a rencontré deux villes d’un même pays jumelées entre elles alors qu’il pensait que c’était impossible. On notera que la notion de fréquence d’un événement n’est pas liée à sa perception d’un point de vue logique. Tant que A considérera qu’il est impossible de jumeler entre elles deux villes françaises, il continuera à s’étonner (même s’il en rencontre tous les jours...). La modalité paradoxale ne consiste pas à s’intéresser à une situation à laquelle on ne s’attendait pas, comme un événement exceptionnel, mais bien à un événement a priori logiquement impossible. En particulier, le fait de vivre la situation de manière fréquente ne la rendra pas acceptable tant qu’une explication logique n’aura pas été trouvée.

4.1.1.2 Modalités (in)désirable et improbable

Si la conversation ne démarre pas sur le mode paradoxal, elle démarrera en présentant une situation rencontrée qui sera considérée par le premier locuteur :

· comme étant agréable ou désagréable. On parlera alors de modalité (in)désirable.

· comme étant un événement a priori improbable (le ‘scoop’). On parlera alors de modalité improbable.

Nous regroupons ici deux modalités apparemment distinctes. La façon de commencer une conversation semble séparer nettement ces deux modalités. Cependant, les possibilités de réponse à une première intervention sur un de ces deux modes sont, sinon identiques, du moins proches. En outre, le second interlocuteur se trompe parfois sur la modalité présentée par le premier. Il arrive même parfois que les deux modalités soit simultanément présentes dès la première intervention du premier locuteur. C’est pour ces raisons que nous les regroupons partiellement.

Nous allons maintenant présenter séparément les modalités (in)désirable et improbable, puis nous montrerons en quoi ces deux modalités se regroupent.

La modalité (in)désirable est caractérisée par le fait que le premier locuteur lance la conversation en présentant un fait qu’il considère comme agréable ou désagréable (le plus souvent, la situation présentée est désagréable). A titre d’exemple, on peut considérer l’extrait suivant [DES 93] (p. 46) :

contexte : A raconte qu’il est en train de repeindre les portes chez lui, et qu’il a décidé de commencer par décaper la vieille peinture, ce qui se révèle être un travail difficile.

A1 - Ben moi, j’en bave actuellement parce qu’il faut que je refasse mes portes, la peinture. Alors j’ai décapé à la chaleur. Ca part bien. Mais pas partout. C’est un travail dingue, hein ?

A indique donc la situation indésirable qu’il rencontre à l’heure actuelle en effectuant un travail fastidieux. On notera ici que A est obligé de donner explicitement la modalité dans laquelle il se place dès le début de son intervention (‘Ben moi, j’en bave...’), car la problématique n’apparaît pas clairement avant la fin de sa réplique (‘C’est un travail dingue, hein ?’).

La modalité improbable est caractérisée par le fait que le premier locuteur entame la conversation en présentant un fait qu’il considère comme inhabituel. A titre d’exemple, on peut considérer l’extrait suivant [DES 93] (p. 23) :

contexte : A parle à son fils C dont la sœur a commandé une nouvelle voiture au début de la semaine.

A1 - Je t’ai dit que B a commandé une nouvelle voiture ?

Dans le contexte (où B achète une voiture par décennie), C peut assigner a priori une probabilité très faible au fait que sa sœur achète une voiture au cours de la semaine. A condition que C n’ait pas été mis au courant avant A1, l’événement que présente A est inattendu pour lui : il s’agit d’un ‘scoop’.

On notera qu’un fait n’étant jamais improbable a posteriori (sachant que le fait est arrivé, sa probabilité est rigoureusement de 1), il faut comprendre le terme ‘improbable’ comme improbable a priori.

Le mode paradoxal n’est pas non plus un mode improbable avec une probabilité a priori nulle. Un événement de probabilité a priori nulle est un événement survenu dans un contexte bien connu par le sujet et qui n’avait jamais été rencontré auparavant dans ce contexte. Un événement paradoxal est un événement qui viole les contraintes logiques que le sujet prête à la situation. En outre, on n’obtient pas les mêmes types de réponses (deuxième intervention et suivantes) en fonction de la modalité de la première réplique. Un sujet présentant une situation paradoxale saura démontrer l’aspect paradoxal de la situation, alors qu’une situation improbable ne pourra être présentée que comme rare.

Les modes improbable et (in)désirable ont par contre une nature commune. La frontière entre ces deux modalités est d’ailleurs suffisamment floue pour autoriser des répliques successives sur les deux modalités. Si l’on considère un espace à deux dimensions, dont l’une est la probabilité a priori, et l’autre la désirabilité/indésirabilité, on peut définir un espace de pertinence et une zone de banalité (cf. figure 4.1).

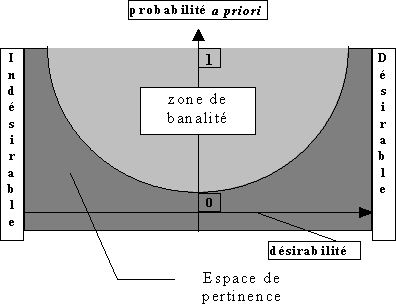
figure 4.1 - Espace de pertinence et zone de banalité

Une réplique sera pertinente dans le cas où la combinaison de sa probabilité a priori et de sa désirabilité la situerait dans l’espace de pertinence. Une réplique située dans la zone de banalité sera donc rejetée.

Cette courbe est obtenue par une extension de la définition de l’information au sens de Shannon. Si on note P la probabilité a priori de l’événement indiqué et D sa désirabilité (entre -1 et 1), l’information apportée par une intervention peut s’écrire :

I(D,P) = |ln(((1-|D|)P)^-1)|

Une intervention sera donc d’autant plus pertinente que P sera proche de 0 et |D| proche de 1. La frontière entre zone de banalité et espace de pertinence est obtenue pour I(D,P) constante, soit pour P(1-|D|) constante. La courbe proposée figure 4.1. n’est cependant indiquée que dans le but d’illustrer notre propos. En effet, la position de la frontière (i.e. la valeur de la constante dans I(D,P)=constante) peut varier d’un individu à l’autre, et même d’une discussion à l’autre. La surface de l’espace de pertinence semble ainsi augmenter avec la proximité des interlocuteurs : démarrer une discussion demande un I(D,P) nettement plus élevé avec quelqu’un que l’on connaît peu qu’avec un ami de longue date.

Une des conséquences de ce lien entre les deux modalités est qu’il sera possible d’introduire une situation qui soit à la fois improbable et indésirable. Cela entraîne un risque de confusion de la part du second interlocuteur, qui peut se ‘tromper’ de mode pour sa réplique. Quand une telle confusion s’opère, le premier intervenant bloque la discussion en explicitant la modalité qu’il présente. En d’autres termes, le second locuteur pourra disposer de deux stratégies pour invalider une réplique pertinente, mais le premier locuteur risque de n’en accepter qu’une seule.

4.1.2 Une succession de réponses pour détruire les problématiques

Une fois la problématique posée, et le contexte défini sans ambiguïté, la conversation proprement dite commence. Chaque participant va à tour de rôle chercher à détruire la validité des arguments des autres interlocuteurs. Le rôle des répliques successives sera soit de détruire ou d’atténuer le caractère problématique de la situation initiale, soit de détruire ou d’atténuer la validité des arguments opposés à la problématique.

Deux stratégies de destruction sont accessibles aux interlocuteurs : l’invalidation logique, qui se présente sous deux formes distinctes, et dont l’objectif est de démontrer de manière logique que la situation n’est pas problématique et l’atténuation, qui peut elle aussi prendre deux formes, et dont l’objectif est de ramener la problématique initiale de l’espace de pertinence dans la zone de banalité.

Le choix de stratégie n’est cependant pas libre. Il dépend en fait de la modalité dans laquelle a voulu se placer le premier interlocuteur :

· S’il s’agit de la modalité paradoxale, les intervenants doivent utiliser l’invalidation logique.

· Pour la modalité improbable, les intervenants ont le choix entre l’invalidation logique et une des deux formes de l’atténuation : la banalisation.

· Pour la modalité indésirable[1], le choix de la stratégie d’invalidation est libre. Les intervenants peuvent utiliser l’invalidation logique et les deux formes de l’atténuation.

4.1.2.1 Invalidations logiques

L’invalidation logique consiste à démontrer que la problématique présentée par le premier interlocuteur est erronée. Il existe pour cela deux manières de procéder. L’invalidation logique directe consiste, tout en acceptant la validité du paradoxe présentée par le premier locuteur, à en nier un de ces termes. L’invalidation logique indirecte consiste à refuser le paradoxe proposé en introduisant un terme (ou prémisse) caché. En d’autres termes, dans le premier cas, le second interlocuteur réfute la perception de la situation, et dans le second cas, il en réfute l’interprétation. Ce type d’invalidation est valable quelle que soit la modalité problématique utilisée.

L’invalidation logique directe consiste simplement à détromper son interlocuteur sur la valeur de vérité d’un des termes intervenant dans la problématique. Cette invalidation est applicable quelle que soit la modalité problématique comme l’illustre l’exemple suivant :

contexte : A appelle B pour qu’il voie un insecte muni d’un étrange appendice.

A1 - Tiens, regarde le dard qu’elle a.

B1 - ça alors !

A2 - C’est marrant.

B2 - C’est pas un dard, c’est une trompe.

La modalité est l’improbabilité, les dards d’insectes étant a priori beaucoup plus court que celui qu’observe A. L’invalidation logique directe (B2) rend le contexte problématique caduc, sans s’attaquer en quoi que ce soit à la validité de l’estimation de l’improbabilité. B indique qu’il serait lui aussi surpris s’il rencontrait un insecte ayant un dard aussi long, mais qu’en l’occurrence, ce n’est pas le cas.

Bien que l’exemple donné ici ne consiste pas en une démonstration, on peut observer des invalidations logiques directes en comprenant une. Considérons par exemple :

contexte : Beaucoup de gens préfèrent acheter des poulets ‘garantis fermiers’ qui sont pourtant beaucoup plus chers. A s’étonne de ce comportement, puisque selon lui ‘garanti fermier’ ne sont que des mots, et non une véritable garantie.

A1 - Alors ce qui impressionne les populations, c’est le mot ‘garantie’. Un gars qui fait des poulets d’élevage, il met garanti fermier, alors tout le monde se précipite.

B1 - Mais il y a des labels.

A2 - Oui, mais garantis par qui ?

B2 - Mais ils le disent, par qui, parfois… Par la chambre syndicale des machins…

La modalité est paradoxale. Le premier interlocuteur considère comme absurde le fait d’acheter des poulets à cause d’une mention qui n’est pas garantie. Le second interlocuteur lui rétorque que la mention est garantie par des labels eux-mêmes garantis. Il invalide donc bien le fait que les labels ne soient pas garantis mais il le fait en démontrant pourquoi. On notera que là encore, B ne s’attaque pas à la validité de l’incompatibilité, mais seulement à la valeur de vérité d’un de ses constituants.

La spécificité de ce type d’invalidation réside justement dans le fait que la problématique n’est pas attaquée. Il s’agit du seul cas où le sujet n’est pas obligé de revoir ses conceptions pour rendre cohérents expérience et connaissance[2]. Les autres types d’invalidation fonctionnent différemment en cela qu’elles ont toutes pour objet de modifier la problématique, amenant ainsi le premier locuteur à modifier ses conceptions. En effet, si le premier locuteur accepte l’invalidation proposée, il devra modifier soit le paradoxe qu’il supposait valide, soit l’estimation de la probabilité a priori de l'événement qu’il a rencontré, soit l’estimation en terme de désirabilité de la situation qu’il rencontre.

L’invalidation logique indirecte consiste à invalider la problématique utilisée en faisant intervenir une prémisse ‘cachée’. Le second interlocuteur considère, quelle que soit la modalité, que la problématique présentée par le premier est incomplète. Un des éléments de cette problématique a été ‘oublié’ par le premier interlocuteur, et le second le lui signale. Bien entendu, la valeur de vérité constatée de ce terme oublié doit être l’inverse de celle apparaissant dans la problématique. Sinon, le rappel de la prémisse cachée ne modifie pas le statut de cette problématique. Nous allons examiner un exemple sur la modalité indésirable (extrait de [CRY 75], page 52) :

contexte : Deux couples britanniques (B et C, A et D) viennent d’échanger leurs expériences de vacances. La discussion arrive sur le meilleur moyen de traverser la Manche. Le Ferry Boat est mentionné comme moyen de transport.

[…]

C5 - I mean taking a car across to the continent on a ferry is… is hell.

A6 - no, it isn’t at all.

[…]

C9 - well I’ll tell you the sort of thing I’ve heard, I mean ev…every summer, you see stories of tremendous queues at the…

D8 - but they’re people who haven’t booked.[3]

C indique donc que traverser la Manche avec sa voiture sur un ferry est insupportable à cause de la queue que l’on doit faire avant d’embarquer. D ne remet pas en cause le caractère indésirable de devoir faire la queue, mais invalide le fait qu’une traversée de la manche en ferry implique une longue queue. Pour D, c’est le fait de traverser en ferry et de ne pas avoir réservé qui implique une longue attente. Bien qu’il ne le précise à aucun moment, il est implicite que D avait effectivement réservé avant de se déplacer (le second principe de pertinence rend inutile la précision de ce fait : l’intervention D8, qui sert d’invalidation à la problématique de C, étant pertinente, il est nécessaire que D ait réservé puisque sinon, la problématique ne serait pas cassée).

On pourrait objecter que l’on est encore en présence d’une invalidation logique directe : A indique simplement à C que traverser la Manche en ferry avec une voiture n’est pas indésirable, contrairement à ce que C affirme. Mais C démontre ensuite pourquoi cette situation est indésirable, et D invalide alors également la démonstration du caractère indésirable de cette traversée. C’est cette seconde invalidation qui est une invalidation indirecte.

Cet exemple met également en lumière le fait que l’aspect indésirable d’une situation soit hérité par ces antécédents logiques : si une situation est jugée indésirable, une situation impliquant cette situation sera également jugée indésirable. C’est ce qui se produit pour C dans l’extrait précédent en C5.

Dans notre exemple, les deux interlocuteurs sont d’accord sur le caractère indésirable de devoir subir une longue file d’attente, mais comme A ne comprend pas la référence que fait C à ce problème, il invalide simplement la proposition de C en A6. En C9, C explicite le caractère indésirable de la traversée en Ferry, ce qui permet à D de fournir l’invalidation correcte D8, mettant ainsi fin à la conversation.

4.1.2.2 Atténuations

L’atténuation[4] consiste à ramener l’intervention du premier interlocuteur de l’espace de pertinence vers la zone de banalité. La modalité incompatible, ne se plaçant pas à l’intérieur de cet espace, n’est donc pas concernée par ce type de stratégie.

On retrouve bien ici les deux principes de pertinence : non seulement le sujet prenant la responsabilité d’une conversation se devra d’être pertinent, mais en outre, ses interlocuteurs n’auront de cesse qu’une fois l’absence de pertinence de sa problématique établie. L’idée de Grice [GRI  75] selon laquelle les interlocuteurs coopèrent au cours d’une conversation semble alors battue en brèche si l’on considère les modalités paradoxales et indésirables : si l’on ne peut pas démontrer à son interlocuteur qu’il dit des choses erronées, on se contente de lui expliquer qu’on les trouve banales, et qu’il était donc inutile de les dire. Cependant, la destruction de la problématique d’un interlocuteur peut-être vécue par celui-ci comme un acte coopératif, puisque cette destruction lui permet de résoudre le problème qui se posait à lui.

L’atténuation peut prendre deux formes : la banalisation, qui consiste à déplacer directement le positionnement de la réplique selon un des deux axes, et l’antagonisation qui consiste à effectuer ce déplacement selon l’axe de la désirabilité de manière indirecte. La banalisation est toujours possible à la fois pour les modalités (in)désirable et improbable, alors que l’antagonisation n’est possible que pour la modalité (in)désirable.[5]

La banalisation consiste pour le second interlocuteur à déplacer directement la réplique du premier interlocuteur vers la zone de banalité : le second interlocuteur montre au premier qu’il n’a pas la même estimation du couple (improbabilité, indésirabilité) et que selon lui, la situation présentée est banale.

La banalisation d’une improbabilité s’effectue en indiquant des situations passées similaires. Le principe consiste à augmenter la probabilité a priori de l’événement initialement présenté comme rare. Le premier locuteur aurait été moins surpris par l’événement qu’il présente s’il avait pris en compte les événements similaires que lui présente le second interlocuteur. Illustrons ceci sur un exemple :

Contexte : Cette conversation intervient après quelques remarques sur le temps qui était assez doux pour permettre aux enfants de jouer dehors. La température semblait exceptionnellement douce pour cette période de Nouvel An.

A1 - De toutes manières, la température qu’on a aujourd’hui, c’est le maximum qu’on puisse espérer jusqu’à, jusqu’à la mi-février !

B1 - Ca c’est vrai.

C1 - Je te dis, moi, en 77 y avait eu un temps de Föhn, l’hiver […] Il faisait 20° au 1^er janvier.

B2 - Je me rappelle une année, quand nous étions petites, je m’en souviens très bien. Le 20 décembre, à peu près. […] On avait, D et moi, des robes… les robes d’été ! Des robes d’été ! Et ça avait été une année vraiment exceptionnelle.

A lance la conversation en remarquant la température anormalement douce pour une période de nouvel an (en fait, A1 est vraisemblablement bimodale, mais B et C attaquent A1 sur l’axe de la probabilité. On peut donc considérer, pour la clarté de l’exemple, que la modalité choisie est l’improbabilité). Il signifie ainsi que les exemples de nouvel an qui lui reviennent en mémoire ne possédait pas une température analogue. La probabilité a priori d’un nouvel an aussi doux est donc selon lui faible. Mais B et C, par C1 et B2, donnent deux instances de nouvel an au moins aussi doux. Si l’on prend en compte les événements fournis en C1 et B2 dans la base d’exemple servant à calculer la probabilité a priori, on diminue nettement le caractère improbable de la situation. A titre d’exemple, et sans prétendre à une quelconque exactitude, si l’on suppose que la base d’exemple est établie sur les 5 dernières années, on passe d’une probabilité a priori quasi-nulle (0 cas sur 5) à une probabilité de l’ordre de 29 % (2 cas sur 7).

On remarque également que la banalisation de B est moins précise que celle de C : B ne se rappelle pas de l’année ni de la température, et utilise des exclamations et des superlatifs pour renforcer la valeur de cette banalisation. Le fait que B se co-réjouisse avec A en B1 avant de banaliser A1 en B2 n’est donc pas surprenant, puisque la banalisation qu’il propose aurait pu être trop faible si elle n’avait été accompagnée de C1.

La banalisation sur le mode indésirable garde le même objectif (contester le positionnement de la réplique dans l’espace probabilité*désirabilité, ici en indiquant un désaccord sur la valeur d’indésirabilité portée par la situation) mais n’utilise pas la même stratégie. Le principe est simplement d’indiquer à l’autre que la situation rencontrée n’est pas ‘si grave que ça’, comme dans l’exemple :

Contexte : A a acheté plusieurs cartes postales qu’il destine à des amis différents, et il a commencé à les écrire.

A1 - Oh zut, je me suis trompée de carte ! J’ai écrit cette carte à C.

B1 - Pff ! Qu’est-ce que ça peut faire ?

La banalisation d’indésirabilité est le cas le plus apparent du positionnement différent d’une réplique par deux interlocuteurs. Elle est même suffisamment courante pour faire son apparition dans la sagesse populaire. ‘Plaie d’argent n’est pas mortelle’ est une banalisation toute faite pour les situations indésirables touchant à l’argent (comme se faire voler son portefeuille par exemple).

L’antagonisation consiste pour le second interlocuteur à présenter les aspects désirables d’une situation jugée indésirable ou les aspects indésirables d’une situation jugée désirable dans de plus rares cas (‘Ne te réjouis pas trop vite…’). L’objectif est de moyenner les aspects négatifs de la situation avec ses aspects positifs, afin que la position de cette ‘moyenne’ se trouve au sein de la zone de banalité. Il s’agit donc d’une atténuation indirecte puisque le second interlocuteur, sans s’attaquer à la réplique du premier, cherche à casser la problématique en faisant intervenir des termes cachés, comme dans l’exemple :

Contexte : Discussion à propos d’un marin français qui concourait pour la Coupe de l’América, en étant supporté par le public français.

A1 - Alors Marc Pajot s’est fait écraser encore.

B1 - Deux minutes, c’est pas écrasé !

A2 - Deux minutes quarante secondes, si.

C1 - Oui, mais enfin, tu sais, hein, il a quand même tenu le coup jusqu’au dernier moment, hein, lui.

A3 - Quel coup ?

C2 - Hé ben enfin, il a pas sombré, il est pas tombé, il est arrivé !

A4 - Tu veux dire qu’il est arrivé, il est arrivé en demi-finale

C3 - En demi-finale, écoute !

La modalité est l’indésirabilité. Après une tentative de banalisation B1 refusée par A2, C tente une antagonisation de C1 à C3, en opposant à la défaite indésirable du marin français l’accession désirable de ce même français au stade des demi-finales.

On remarquera le parallèle entre la banalisation et l’invalidation logique directe d’une part, et entre l’antagonisation et l’invalidation logique indirecte d’autre part. Dans le premier cas, l’attaque de la problématique est basée sur la validité des arguments (sur la valeur de vérité des termes de la problématique pour l’invalidation logique directe et sur l’estimation du positionnement de la réplique dans l’espace probabilité*désirabilité dans le cas de l’atténuation), alors que dans le second elle porte sur la validité de la problématique elle-même, en indiquant, tant pour l’invalidation logique indirecte que pour l’antagonisation, une partie de la situation ‘oubliée’ dans la présentation de la problématique par le premier interlocuteur.

On remarquera enfin que l’antagonisation elle aussi est suffisamment fréquente pour être passée dans la sagesse populaire. Ainsi l’expression ‘A quelque chose, malheur est bon’ peut-être considérée comme l’archétype des antagonisations, puisqu’elle s’applique à toutes les situations indésirables.

4.2 Les trois modalités

Nous présentons maintenant la modélisation tirée de l’étude menée par J.-L. Dessalles. Pour chaque modalité, nous proposons la représentation choisie, les différentes opérations de calcul de répliques et les utilisations pratiques rendues possibles par cette modélisation. Nous terminons ce paragraphe en introduisant une nouvelle manière de représenter les règles, en utilisant les notions de noyau et de menu.

4.2.1 La modalité incompatible

Nous abordons ici la représentation de la modalité ‘incompatible’. Nous nous intéressons d’abord à la représentation à adopter pour les connaissances logiques. Nous abordons ensuite le calcul de réplique rendant compte des résultats présentés en 4.1, et nous terminons par une présentation rapide du principe de fonctionnement de SAVANT-3, un système critique construit en s’appuyant sur les résultats que nous venons de présenter.

4.2.1.1 Représentation de la modalité incompatible

La représentation des connaissances logiques va se faire sous la forme de règles. La règle (A, B et C incompatibles) se notera pour nous :

(A, B, C) Þ Faux

Ainsi, l’exemple vu en 4.1.1.1, (‘tout à l’heure, j’ai vu une ville jumelée avec une ville d’Alsace’) se traduira par :

(jumelées(Ville A, Ville B), non(étrangères(Ville A, Ville B))) Þ Faux

Cette notation constitue une réécriture de la logique du premier ordre[6] sous la forme normale conjonctive négative. Elle respecte donc toutes les propriétés de la logique du premier ordre en terme de validité, complétude, … tout en étant mieux adaptée à la représentation des règles logiques utilisées dans une conversation. A titre d’exemple, l’implication se notera :

(A Þ B) devient ((A, non B) Þ Faux)

On remarque que la notation classique nécessite d’expliciter la contraposée (pour l’implication précédente (non B Þ non A)) alors que cela est inutile avec notre notation puisque chaque règle est sa propre contraposée.

Afin de modéliser la connaissance logique d’un individu, il faut donc maintenir :

· Une base de règles d’incompatibilité. Chaque règle prenant la forme d’une conjonction de clauses impliquant Faux.

· Une mémoire permettant de conserver les valeurs de vérité estimées pour les termes intervenant dans les règles.

Le lecteur aura remarqué que la disjonction n’intervient pas au sein d’une clause. Est-ce à dire que les règles d’incompatibilité sont en disjonction les unes par rapport aux autres ? La réponse est non, et les connaissances d’un individu s’expriment sous la forme d’une conjonction de clauses. C’est l’expression des règles sous forme d’incompatibilité qui masque la disjonction. Dire que A et B sont incompatibles revient à dire que dans toute situation A ou B est faux. Dire que (A ou B) est incompatible revient à dire que A est incompatible et que B est incompatible.

Nous appellerons ‘Fait’ les couples (terme, valeur de vérité). Il existe trois manières de représenter un fait dans notre modélisation, à savoir les hypothèses, les faits contingents et les faits non contingents. De manière plus détaillé, cela donne :

· Les hypothèses seront simplement stockées dans la mémoire prévue à cet effet. Leurs valeurs de vérité seront susceptibles de changer au cours d’une conversation (par exemple : (‘il fait beau’, vrai)).

· Les faits contingents se représenteront sous la forme d’une règle d’improbabilité à terme unique. De tels faits seront supposés vrais en règle générale, mais pourront être remis en cause au cours d’une conversation, notamment pour fournir une invalidation logique indirecte.

· Les faits non contingents se représenteront sous la forme d’une règle d’incompatibilité à terme unique. Leurs valeurs de vérité ne peuvent pas changer au cours d’une conversation, et l’évocation de leur négation entraîne une détection d’incompatibilité (par exemple : ((‘la terre est plate’, vrai)) Þ Faux). Ce troisième type de fait correspond à ce que Sperber et Wilson appellent des hypothèses factuelles dans [SPE 89] (pp. 116-117).

On notera qu’un locuteur n’acceptera jamais la négation d’un fait non contingent. Pour nier un tel fait, il faudra préalablement effectuer une invalidation logique indirecte de la règle portant ce fait.

Il serait tentant de vouloir regrouper les hypothèses et les faits, dans un souci de parcimonie. Cependant, une hypothèse est un élément présent en mémoire de travail et dont on peut à loisir modifier la valeur de vérité, alors qu’une règle (à terme unique ou pas) ne peut être aisément modifiée, n’est pas présente en mémoire de travail, et n’est pas toujours visible (nous verrons au paragraphe 4.3.1 que les règles se comportent comme des alarmes). Ainsi, la règle ((A, B) Þ Mod) reste silencieuse (ou invisible) tant que A et B ne sont pas connus comme vrais, mais détecte et signale le problème quand on suppose (A, vrai) et (B, vrai). De la même manière, la règle ((A) Þ Mod) reste silencieuse tant que A n’est pas connu pour vrai.

4.2.1.2 Calcul de répliques

A partir de la représentation choisie, on peut, à la présentation d’une contradiction :

· Nier un des termes présents dans la contradiction. Il suffit pour cela d’inverser la valeur de vérité du terme choisi. Si une autre contradiction se fait jour, on itère ce processus, jusqu’à ce que la cohérence soit rétablie (il est toujours possible de rétablir la cohérence d’une situation, sous la condition que la base de règles ne soit pas incohérente). Il s’agit de l’invalidation logique directe.

· Exhiber un terme caché. Cela consiste à considérer que la règle présentée est incomplète, et qu’il faut y rajouter un terme. Ceci n’est possible que si une règle plus complète est connue, ce qui impose des contraintes sur la structure des règles (nous reviendrons sur ce point au paragraphe 4.2.4).

Ces deux stratégies ont été mises à profit pour la réalisation de Savant-3, système critique dédié à l’apprentissage de concepts, que nous présentons maintenant.

4.2.1.3 Savant-3

Nous présentons ici la version de Savant-3 de 1988, développée par Jean-Louis Dessalles [DES 93] (pp. 199-208). Une version réactualisée a été réalisée, dans le cadre de mes travaux, en 1996 au sein de la société CYBEL. Cette deuxième version est présentée au paragraphe 8.1.

Savant-3 est un système critique dédié à l’apprentissage de concepts. Son principe de fonctionnement est de présenter à l’étudiant un contexte argumentatif organisé autour d’une contradiction. L’objectif est de faire réaliser à l’étudiant cette contradiction, lui permettant ainsi de comprendre les liens existant entre les concepts qu’il manipule.

En début d’interaction, la situation n’est pas incohérente. Savant-3 demande à l’étudiant de prendre position sur les éléments de la situation envisagée (par question et dialogue) jusqu’à ce qu’une contradiction se fasse jour, contradiction que Savant-3 va présenter sous la forme d’un étonnement. Une fois la contradiction détectée, l’étudiant est amené à modifier ses positions afin de rétablir la cohérence de la situation. En fait, Savant-3 peut s’étonner à tort. Afin de permettre à l’étudiant d’avoir raison contre le système, et ainsi éviter que les interventions de ce dernier soient considérées comme des sanctions, Savant-3 peut volontairement ‘oublier’ un des termes d’une règle [DES 91b]. Il est alors loisible pour l’étudiant de casser le paradoxe proposé par Savant-3 en utilisant une invalidation logique indirecte. En d’autres termes, l’étudiant peut casser un paradoxe sans revenir sur ses affirmations précédentes.

A titre d’exemple, considérons l’extrait suivant, qui traite de la périodicité d’une sinusoïde discrète cos(2pF₁ n). Ce signal est périodique si et seulement si F₁ est rationnelle. Dans l’extrait, (M) indique une intervention de la machine et (E) une réplique de l’étudiant. Les réponses entre crochets indiquent un choix fermé.

M1 : Le signal cos(2pF₁ n) (pour F₁ donnée) est-il périodique ?

E1 : oui

M2 : D’après ce que j’ai compris : le signal cos(2pF₁ n) (pour F₁ donnée) est périodique.
On pourrait prendre par exemple F₁ = ½p.

E2 : oui

M3 : mais encore ?…

E3 : ça fait cos(n)

M4 : Peut-on dire que cos(n) est périodique ?

E4 : [non]

M5 : Attendez… D’après ce que vous m’avez dit :
- le signal cos(2pF₁ n) (pour F₁ donnée) est périodique
- cos(n) n’est pas périodique
Je m’avoue quelque peu surpris !

E5 : F₁ doit être entière

M6 : D’après ce que j’ai compris : F₁ est un entier. cos(2pF₁ n) risque de ne pas beaucoup ressembler à une sinusoïde !

E6 : pourquoi ?

M7 : Mais cela pose un problème… sauf si vous considérez que cos(2pF₁ n) est un signal constant…

E7 : F₁ doit être l’inverse d’un entier

M8 : oui… mmm… D’accord…

Savant-3 utilise un moteur en chaînage arrière pour essayer d’obtenir la détection d’une situation paradoxale. Une situation sera considérée comme paradoxale par Savant-3 quand au moins une des règles de la base de règle aura tout les termes qu’elle contient connus pour vrai. Considérons la règle d’incompatibilité suivante, utilisée dans l’extrait présenté ci-dessus (le chiffre entre parenthèse indique si la règle est a priori connue par l’élève (règle de ‘bon sens’, valeur 1) ou non (valeur 0)) :

règle 2 (0) :

(La fréquence F₁ est rationnelle, vrai)

(Le signal cos(2pF₁ n) (pour F₁ donnée) est périodique, faux)

Cette règle permettra de détecter une situation incohérente quand l’utilisateur aura affirmé, ou quand, à partir des affirmations de l’utilisateur Savant-3 arrivera à démontrer, que la fréquence F1 est rationnelle et que le signal cos(2pF₁ n) (pour F₁ donnée) n’est pas périodique.

Afin d’effectuer le chaînage arrière, Savant-3 choisit une règle, en extrait un terme P dont la valeur de vérité est inconnue, puis cherche à démontrer P. Pour démontrer P, il recherche ØP dans une règle de la base. Si (ØP Þ Faux) est une règle de la base, la démonstration réussit. Si ØP est trouvée dans une règle en conjonction avec d’autres termes, le moteur cherche à démontrer ces termes sans utiliser P ni ØP. Enfin, si ØP n’est présente dans aucune des règles, la démonstration échoue. Savant-3 fonctionne donc en monde ouvert : pour un terme donné P, la démonstration de P et celle de ØP peuvent échouer toutes deux.

L’objectif initial de Savant-3 était de construire un système capable d’enseigner des connaissances conceptuelles (ou de corriger des fautes conceptuelles) d’une manière naturelle, par le dialogue. Or, si la partie correspondant à la résolution des contradictions suit bien les principes du dialogue présentés plus haut, la phase de mise en contexte en est très éloignée. Au lieu d’introduire une problématique sous la forme d’un étonnement, Savant-3 demande à l’élève de prendre position sur la valeur de vérité d’un terme. Des interventions de ce type ne sont cependant pas acceptables pour débuter un dialogue. Il est par exemple impossible de débuter spontanément une discussion par une réplique comme ‘Le signal cos(2pF₁ n) (pour F₁ donnée) est-il périodique ?’.

C’est afin de résoudre ce problème de mise en contexte qu’une seconde version de Savant-3 a été développée. Cette seconde version, que nous présentons en 7.2, est construite en tant que système critique d’une autre application (généralement un exercice que l’étudiant doit résoudre). Savant-3 espionne son application cliente, et n’intervient que quand il détecte une contradiction dans les actions de l’élève. La mise en contexte est donc effectuée au cours de la résolution de l’exercice. L’idée selon laquelle les interventions de Savant-3 ne doivent pas être perçues comme des sanctions n’est cependant pas nécessairement perdue. Il est en effet toujours possible de faire intervenir Savant-3 par anticipation. Cette fonctionnalité n’a cependant pas été implantée dans cette version, par crainte de voir les élèves perdre confiance dans le système (un élève connaissant bien un domaine ne se verrait alors opposer que des paradoxes invalides).

La représentation que nous avons utilisée pour la modalité incompatible peut de manière aisée s’étendre aux modalités (in)désirable et improbable, ce que nous allons faire dans les deux chapitres suivant.

4.2.2 La modalité (in)désirable

Nous abordons maintenant la représentation de la modalité ‘indésirable’. Nous nous intéresserons d’abord à la représentation à adopter pour cette modalité, en nous appuyant sur la représentation de la modalité incompatible. Nous aborderons ensuite le calcul de réplique, et nous terminerons en montrant la possibilité d’utiliser cette modalité comme un moyen de représenter les objectifs d’un sujet en situation de résolution de problème.

4.2.2.1 Représentation de la modalité (in)désirable

La représentation de la modalité indésirable se fait également sous forme de règles. Ainsi, la situation où A, B et C sont simultanément indésirables se notera pour nous :

(A, B, C) Þ Ind

Ainsi, l’exemple ‘Ben moi, j’en bave actuellement parce qu’il faut que je refasse mes portes, la peinture. Alors j’ai décapé à la chaleur. Ca part bien. Mais pas partout. C’est un travail dingue, hein ?’ se traduira par :

(décaper(porte), outil(chaleur)) Þ Ind.

La modalité indésirable se représente donc comme la modalité paradoxale (cf. 4.2.1.1.). Afin de modéliser la connaissance logique d’un individu en intégrant la modalité paradoxale, il faut donc maintenir :

· Une base de règles d’incompatibilité et d’indésirabilité. Chaque règle prenant la forme d’une conjonction de termes impliquant Faux ou Ind. [7]

· Une mémoire permettant de conserver les valeurs de vérité estimées pour les termes intervenant dans les règles.

On remarquera que sur l’exemple précédent, la notation utilisée est un raccourci de la problématique introduite par le locuteur. Une notation exacte de la problématique serait plutôt :

(refaire(porte), non décaper(porte)) Þ Faux (1)

(décaper(porte), outil(chaleur), non travail(dingue)) Þ Faux (2)

(travail(dingue)) Þ Ind (3)

outil(chaleur) : vrai (4)

refaire(porte) : vrai (5)

Cependant, on peut à partir de cette notation de la problématique retrouver la notation précédente :

De (1) et (5), on déduit décaper(porte) : vrai (6)

De (2), (4) et (6), on déduit travail(dingue) : vrai (7)

De (7) et (3), on déduit Ind

Ainsi, et en considérant que les règles d’indésirabilité/incompatibilité sont communes aux deux interlocuteurs, la problématique proposée par l’intervention se résume en[8] :

((4), (5)) Þ Ind (8)

Soit :

(décaper(porte), outil(chaleur)) Þ Ind

Ce mécanisme d’héritage (les antécédents d’une situation indésirable sont indésirables) est également présent dans l’extrait concernant la traversée de la manche en Ferry, comme nous l’avons vu au paragraphe 4.1.2.1 (nous verrons par la suite que ce mécanisme peut également être appliqué pour les autres modalités et qu’il peut même devenir un mécanisme de compréhension de nouvelles règles).

4.2.2.2 Calcul de répliques

Les mécanismes de calcul de réplique pour la modalité paradoxale (nier un terme de la problématique ou proposer une règle plus précise afin d’effectuer une invalidation logique indirecte) restent valables pour la modalité indésirable. Il est également possible de nier l’aspect indésirable de la situation, afin d’obtenir l’explicitation du contexte dans le cas où la problématique serait présentée dans sa forme compilée (formule (8) de l’exemple précédent, au lieu de {(1), (2), (3), (4), (5)})[9]. Dans le cas d’une modalité indésirable, on peut également :

· Tenter d’atténuer le caractère indésirable de la situation. Cela suppose que l’on soit capable de quantifier (au moins par paliers) l’indésirabilité de la situation. Certaines situations sont trop indésirables pour qu’il soit décent de tenter une atténuation.

· Montrer le caractère désirable de la situation. Il est pour cela nécessaire de disposer de règles de désirabilité. Il faut également être capable de quantifier l’aspect indésirable de la situation présentée, ainsi que l’aspect désirable que l’on met en avant.

· Montrer que la négation de la situation présentée est également indésirable. Là encore, il faut être capable de vérifier que l’indésirabilité de la situation présentée et de sa négation ont un poids comparable, sans quoi l’invalidation sera au mieux inopérante et au pire choquante.

La nécessité de donner un poids aux situations désirables et indésirables rend difficile l’utilisation de ce type de calcul de réplique dans une application informatique. Ainsi, le système Paradise [DES 91a], développé par Jean-Louis Dessalles en 1990 pour simuler des conversations, utilise les modalités indésirable et incompatible, mais ne calcule ses répliques que par le biais des invalidations logiques. Son principe de fonctionnement étant proche de celui de Savant-3, nous ne le présenterons pas plus longuement ici.

4.2.2.3 Une manière de représenter les objectifs

La modalité indésirable permet également de représenter un objectif dans une situation de résolution de problème. Si le sujet cherche à atteindre un état E, on pourra le noter sous la forme :

non(E) Þ Ind

Il peut paraître étonnant que la modalité utilisée soit la modalité Indésirable, alors qu’il paraîtrait plus simple d’utiliser la modalité désirable, en écrivant :

E Þ Dés

Mais cette notation n’est pas la contraposée de la notation présente. Elle indique que pour le sujet, la réalisation de l’événement E suffit à le satisfaire. Mais elle n’indique rien quand E n’est pas réalisé. En d’autres termes, la réalisation de E n’est pas nécessaire à la satisfaction du sujet, et ne constitue donc qu’une faible motivation pour effectuer une action. La notation correcte utilisant la modalité désirable serait (Dés Þ E), mais cette notation ne restitue pas l’idée que les règles fonctionnent comme des alarmes. Elle est donc pour nous inadéquate.

A titre d’exemple, lors d’une résolution de la tour de Hanoï (cf. 7.1.1.), si l’objectif courant est de mettre le disque 5 en C, on pourra noter :

non(Disque(5,C)) Þ Ind

Une manière simple de lire cette notation pourrait être ‘Le problème, c’est que le disque 5 n’est pas en C’.

4.2.3 La modalité improbable

Nous abordons maintenant la représentation de la modalité ‘improbable’. Nous nous intéresserons d’abord à la représentation à adopter pour cette modalité. Puis nous aborderons le calcul de réplique, et nous terminerons en montrant que la modalité improbable permet de mieux expliquer le fonctionnement des invalidations logiques indirectes.

4.2.3.1 Représentation de la modalité improbable

La représentation de la modalité improbable est conforme à celles adoptées pour les modalités indésirable et incompatible. On notera donc (A, B et C improbables) par :

(A, B, C) Þ Imp

Toutefois, cette notation est imprécise, au sens où elle n'indique pas à quel point cette situation est improbable. Mais comme l’utilisation que nous ferons de la modalité improbable n’utilise pas une telle précision, nous nous contenterons de cette approximation. Ainsi, l’exemple vu précédemment ‘Je t'ai dit que B a commandé une nouvelle voiture ?’, se traduira par :

(commander(B, nouvelle voiture, récemment)) Þ Imp

On notera que le terme 'récemment' n'apparaît pas dans l'intervention du premier locuteur, mais qu'il est induit par le principe de la pertinence conversationnelle. L'intervention ne serait pas pertinente si l'achat n'était pas récent, la probabilité a priori d’acheter une voiture sur une période longue étant élevée. Pour s'en convaincre, il suffit d'imaginer (ou d'expérimenter…) la réaction d'un proche si l'on démarrait une conversation par : "Je t'ai dit que B a commandé une nouvelle voiture en 1984 ?".

Afin de modéliser la connaissance logique d’un individu intégrant les trois modalités, il faut donc maintenir :

· Une base de règles d’incompatibilité, d’indésirabilité et d'improbabilité. Chaque règle prenant la forme d’une conjonction de clauses impliquant Faux, Ind ou Imp.

· Une mémoire permettant de conserver les valeurs de vérité estimées pour les termes intervenant dans les règles.

4.2.3.2 Calcul de répliques

Les mécanismes de calcul de réplique pour la modalité paradoxale (invalidation logique directe (nier un terme) ou indirecte (apporter une règle plus précise)) restent valables pour la modalité improbable. Il est également possible de tenter d’atténuer le caractère improbable de la situation. Pour cela, il faut présenter des situations comparables où l'événement improbable survient. Permettre à un système informatique la banalisation d’improbabilités nécessite de lui fournir une base d’expérience lui permettant de rappeler à l’utilisateur des situations analogues à la situation à banaliser. Une expérimentation a été effectuée en ce sens, en utilisant une base de données météorologiques [MUH 99].

4.2.3.3 La modalité «improbable» en tant que modalité «incompatible»

Il reste cependant possible d’utiliser la modalité improbable en tant que modalité incompatible affaiblie, et ce afin de faciliter la représentation d’une prémisse cachée dans le cas de l’invalidation logique indirecte. Une invalidation logique indirecte n’est en effet possible que quand la problématique proposée est une simplification de la problématique réelle obtenue en ignorant un des termes de la problématique. Considérons le paradoxe (A Ù B Ù C) Þ Faux, et sa version simplifiée (A Ù B) Þ Faux. La version simplifiée de la règle, utilisée seule, permettrait de comprendre le paradoxe «A et B», mais ne permettrait pas de fournir l’invalidation  «non C», alors que la version complète de la règle utilisée seule permettrait de trouver l’invalidation, mais ne permettrait pas de comprendre pas le problème (dans ce second cas, la présentation de «A et B» serait vécue comme dénuée de pertinence, puisque aucune problématique ne serait détectée). Seule l’utilisation conjointe des deux règles permet de modéliser les invalidations logiques indirectes.

Une manière de réaliser ceci est de considérer la version complète de la règle, accompagnée de (non C) Þ Improbable. Dans ce cas, il devient possible de comprendre dans un premier temps quelle est la problématique, en supposant (C : vrai), qui correspondra à l’habitude, puis de fournir l’invalidation en proposant (C : Faux).

Nous venons de voir qu’une invalidation logique indirecte ne peut se produire que si le locuteur ayant proposé la problématique à oublié un des éléments de cette problématique. Cet oubli peut-être dû au fait que le sujet ne connaît pas l’existence de cet élément, comme dans l’exemple sur les files d’attentes. Mais cet oubli peut également se produire parce qu’usuellement, l’élément en question est faux. A titre d’exemple, considérons :

Contexte : En voiture à la sortie de Bruges, en Belgique, il s’agit de trouver la route qui mène à Lille afin de rentrer en France. Lille n’est indiquée nulle part, alors que d’autres villes (par exemple Risjel), nécessairement petites puisqu’elles ne figurent pas sur la carte du sujet sont abondamment fléchées.

A1 - Ils ont une ville d’un million d’habitants à soixante kilomètres et ils ne la flèchent même pas.

L’intervention A1 se traduit par :

(proche(Ville), importante(Ville), non fléchée(Ville)) Þ Faux (1)

La solution de ce problème réside dans le fait que Risjel signifie Lille en Flamand. En (1), A a identifié son incapacité à voir un fléchage à son absence, en utilisant :

(fléchée(Ville), non voir(FléchageVille)) Þ Faux (2)

voir(FléchageVille) : Faux (3)

Ce qui l’amène à déduire :

fléchée(Ville) : Faux (4)

Mais la règle (2) est incomplète car elle contient un terme caché. Une écriture correcte de (2) est :

(fléchée(V), non voir(FléchageVille), fléchage(français)) Þ Faux (2’a)

(non fléchage(français)) Þ Imp (2’b)[10]

Si l’on considère l’improbabilité comme une incompatibilité, on déduit de (2’b) que le fléchage est en français, et (2’a) se comporte alors comme (2).

Il est possible de mettre à profit ce comportement des clauses improbables pour représenter des termes cachés dans un système à la Savant-3. Les règles d’improbabilités seront dans un premier temps considérées comme des règles d’incompatibilité, mais elles pourront être ignorées quand il n’existe pas d’autre moyen de sortir de la situation paradoxale dans laquelle on se trouve. Dans la version que nous avons présentée, le système Savant-3 peut s’étonner trop tôt en ‘oubliant’ un terme quelconque d’une règle. Ceci donne de mauvais résultats, car il peut ‘oublier’ un terme essentiel et son étonnement n’est pas toujours compréhensible par l’utilisateur. Dans l’exemple que nous venons de traiter, il pourrait ignorer le terme (non fléchée(Ville)) et s’étonner du paradoxe (proche(Ville), importante(Ville)) Þ Faux qui indique qu’il est incompatible pour une ville d’être à la fois proche et importante ! L’utilisation de la modalité improbable permettrait de corriger ce défaut. Nous avons également développé une deuxième méthode pour contourner ce problème dans nos simulations, en utilisant les notions de noyau et de menu, que nous allons présenter maintenant.

4.2.4 Utilisation d’un noyau et d’un menu

L’examen de l’invalidation logique indirecte montre une différence qualitative entre différents termes d’une règle. Tout se passe comme si certains termes pouvaient être oubliés et d’autres pas. Comme nous venons de le voir, ce mécanisme peut s’expliquer par l’utilisation de la modalité improbable. Cependant, l’utilisation dans une réalisation informatique de cette modalité nécessite de connaître la probabilité a priori de chacune des règles d’improbabilités. Il faut en outre doter le système de mécanisme de mise à jour de ces valeurs de probabilité a priori. Or, si l’on ne s’intéresse qu’au fait de savoir si une partie d’une règle est ou non susceptible d’être oubliée, on peut se placer dans un cas binaire : un terme donné est ou n’est pas susceptible d’être oublié. Nous présentons ici un mécanisme plus simple qui permet de simuler ce comportement. Pour ce faire, nous introduisons un complément à notre représentation des règles, qui se décomposeront en deux parties : le noyau et le menu.

Précisons à nouveau que l’utilisation du noyau et du menu constitue une simplification de notre modèle complet, au sens où elle nous permet de faire l’économie de la modalité improbable dans la suite de notre travail, puisque nous n’utilisons cette modalité que pour expliquer l’invalidation logique indirecte. La modalité improbable intervient dans les conversations, et certains des mécanismes qui y sont attachés, comme l’antagonisation, ne peuvent s’expliquer si on la supprime. Nous disposons donc de deux modèles concurrents, et nous retiendrons le modèle avec noyau et menu car il est suffisant pour la suite de notre travail.

4.2.4.1 Retour sur l’invalidation logique indirecte

L’invalidation logique indirecte consiste à mettre à jour une clause ‘oubliée’ d’une règle. Mais toutes les clauses d’une règle ne sont pas susceptibles d’être oubliées. Ainsi, dans l’exemple concernant le fléchage de Lille en Belgique, la règle complète utilisée pour produire l’invalidation est :

(fléchée(V), non voir(FléchageVille), fléchage(français)) Þ Faux

La clause oubliée est :

fléchage(français)

Ce qui donne la règle :

(fléchée(V), non voir(FléchageVille)) Þ Faux

Les deux autres termes de la règle ne sont pas susceptibles d’être oubliés, car l’oubli de l’une d’entre elle ne crée pas un paradoxe acceptable, comme dans :

(fléchée(V), fléchage(français)) Þ Faux

Il suffit pour s’en convaincre d’expérimenter la chose, en débutant une conversation avec un proche par «Ce matin, j’ai vu un panneau de signalisation en langue française».

Afin de représenter la différence entre les clauses susceptibles d’être oubliées et celles qui ne le sont pas, nous allons utiliser un artifice de représentation en scindant nos règles en deux parties : le noyau et le menu.

4.2.4.2 Définitions du noyau et du menu

Nous appellerons noyau d’une règle l’ensemble des termes d’une règle qui ne sont pas susceptibles d’être oubliés. Nous appellerons menu d’une règle l’ensemble des termes susceptibles de compléter le noyau. Le menu est l’union ensembliste des invalidations logiques indirectes possibles de la règle constituée par le noyau. Cet ensemble est nécessairement fini puisque les règles représentent la connaissance logique d’un individu le sont : une invalidation logique indirecte n’est possible que si la règle complète est connue par le sujet. Le menu comprend donc l’ensemble des exceptions à la règle que connaît le sujet, et cet ensemble est fini. De fait, une règle dont le menu comporte N invalidations regroupe N règles au sens du paragraphe 4.2.3.1. Une manière de voir les notions de noyau et de menu est de considérer qu’il s’agit d’une écriture condensée d’un ensemble de règles.

Par construction, une règle sous la forme (noyau, menu) permet d’expliquer l’invalidation logique indirecte. La problématique est détectée dès que chacun des termes du noyau est connu pour avoir la valeur de vérité avec laquelle il intervient dans ce noyau. Dès qu’un des termes du menu est faux, la problématique est résolue.

Afin de représenter une règle décomposée en noyau et menu, nous utiliserons la notation :

[Noyau, Menu] Þ MOD

ou Noyau sera la liste des termes en conjonction constituant le noyau, et Menu sera la liste des invalidations possibles de la règle. Menu sera donc une liste de liste de termes, afin de pouvoir représenter les invalidations comportant plusieurs termes. Ainsi, la notation :

[[A Ù B], [[C], [D]]] Þ MOD

décrira la règle de noyau «A et B», de menu comportant deux invalidations distinctes «non C» et «non D», et de modalité MOD alors que la notation :

[[A Ù B], [[C, D]]] Þ MOD

décrira la règle de noyau «A et B», de menu comportant une unique invalidation «non (C et D)», et de modalité MOD. On notera que les invalidations logiques possibles sont les négations des conjonctions de terme intervenant dans le menu. Cela est normal puisque la sémantique d'une règle est d'exprimer une contradiction pragmatique[11]. Le menu est donc constitué de la liste des négations d'exceptions de la règle exprimée par le noyau.

Notons enfin que si l’on ne s’intéresse qu’à la capacité des termes à être ou non oubliés, le modèle par noyau et menu et le modèle par la modalité improbable sont équivalents. Ainsi, la règle :

[[A Ù B], [[C], [D]]] Þ MOD

peut se réécrire :

(A, B, C, D) Þ MOD

avec :

(non C) Þ Imp

(non D) Þ Imp

Ces deux modélisations se comporteront de la même façon. En effet, la problématique MOD sera détectée dès que A et B seront connus à vrai, et elle sera résolue dès que C ou D seront connus à faux. Ces deux modélisations ne différeront dans leur comportement que si l’on s’intéresse à la valeur d’improbabilité de C et D, ce qui ne sera pas le cas dans la suite de ce travail. La simplification que nous avons effectuée est donc légitime.

4.2.4.3 Retour sur la représentation des connaissances

Afin de modéliser la connaissance logique d’un individu intégrant les trois modalités, il faut finalement maintenir :

· Une base de règles d’incompatibilité et d’indésirabilité. Chaque règle étant constituée :

• d’une des deux modalités paradoxale ou (in)désirable.

• d’un noyau, constitué d’une conjonction de termes.

• d’un menu, constitué d’un ensemble de termes pouvant séparément venir compléter le noyau.

· Une mémoire permettant de conserver les valeurs de vérités estimées pour les termes intervenant dans les règles. Chacun des termes sera mémorisé avec sa valeur de vérité et sa nature (fait connu ou fait contre-factuel).

4.3 Les mécanismes de fonctionnement de la partie logique du modèle

Nous venons d’examiner dans le détail les conséquences que l’on peut tirer d’une observation de conversations spontanées. Nous en avons conclu qu’au sein d’une conversation, chaque réplique a pour rôle de détruire ou de défendre la problématique qui a été proposée en début de conversation. Nous avons également fait apparaître trois modalités (paradoxale, indésirable et improbable), et nous avons pour chacune d’entre elles proposé une manière de les représenter. Nous avons également examiné quels processus spécifiques pouvaient s’appliquer pour chacune des trois modalités.

Nous allons maintenant proposer les mécanismes de fonctionnement de la partie logique de notre modèle que nous tirons de cette étude, en indiquant comment ces mécanismes permettent de représenter les comportements observés. Notre modèle autorise deux types de manipulations :

• Détecter une contradiction ou une incompatibilité. Nous parlerons de détection d'une "saturation".

• Produire un "contre-factuel" en situation de blocage.

4.3.1 Détection de saturation

Comme l'étude de Dessalles le montre, un sujet est capable de détecter de manière systématique une contradiction ou une indésirabilité. Ces détections fonctionnent de manière identique pour les deux modalités. Afin de modéliser ce comportement, nous utiliserons des règles logiques qui se comporteront comme des détecteurs de ‘saturation’. Considérons en notant MOD la modalité (Faux ou Ind) :

[[A Ù B Ù … Ù X],[[N] Ù [M] Ù … Ù [Y]]] Þ MOD

Cette règle amènera une détection de la modalité quand, et seulement quand, chacun des termes du noyau de la règle sera connu pour vrai, et quand aucun des termes intervenant dans une des invalidations du menu ne sera connu pour faux. Dans cette situation, nous dirons que la règle ‘sature’.

A titre d'exemple, la règle [[A, B, non C], [[D]]] Þ MOD saturera quand, et seulement quand, A sera connu pour vrai, B pour vrai, non C pour faux (et donc C vrai) et que D sera soit connu pour vrai, soit inconnu.

Nous considérons que le fonctionnement des règles est assimilable à des fonctionnements «d’alarme» : une règle reste invisible tant que le noyau n’est pas saturé (comme un détecteur d’incendie reste silencieux tant qu’il n’y a pas de fumée, d’où le nom «d’alarme»). Quand le noyau est saturé, et si aucun des éléments du menu n’est connu pour faux, la modalité associée à la règle est détectée (et les différents éléments du menu deviennent alors des candidats pour effectuer une invalidation logique indirecte). On notera que dans le cas où un des éléments du menu est connu pour faux, la règle ne peut plus saturer et la détection n’a donc pas lieu.

Une conséquence importante de la définition de la saturation est qu'une règle contenant un terme, du noyau ou du menu, connu pour faux ne pourra pas saturer. Dans une telle situation, nous dirons que la règle est ‘invalidée’. La règle [[A, B, non C], []] Þ MOD sera ainsi invalidée dès que A ou B seront connus pour faux ou C pour vrai. [12]

Pour la modalité paradoxale, une troisième situation particulière est à noter pour les règles à menu nul. Dans le cas où tous les termes du noyau de la règle sauf un sont connus pour vrai, et où la valeur de vérité du dernier terme n’est pas encore connue, il est possible de déduire cette valeur. En effet, si ce dernier terme est vrai, la règle sature et on obtient une contradiction. Il faut donc que ce terme soit faux. Dans une telle situation, nous dirons que la règle ‘déclenche’.

A titre d’exemple, la règle [[A, B, non C], []] Þ MOD déclenchera dans le cas ou A et B seront connus pour vrai (ainsi que dans les cas (A vrai, C faux) et (B vrai, C faux)).

Nous ne postulons pas la possibilité pour un sujet d'effectuer ce dernier type d'opération de manière systématique. Le terme inconnu n'est pas nécessairement envisagé par le sujet, pas plus que la règle déclenchante. Nous n’intégrerons donc pas une capacité de ce type dans notre modèle. Nous tirerons par contre avantage de cette propriété afin de doter nos systèmes critiques de capacités de déductions.

Nous allons maintenant examiner les possibilités offertes par la détection de saturation pour la modalité incompatible puis pour la modalité indésirable.

4.3.1.1 Des capacités d’inférence : reductio ad absurdum

Le fait de ne pas utiliser la détection de déclenchement ne prive pas notre modèle de capacités de déduction. En effet, si le terme inconnu est envisagé, le modèle peut affecter une valeur de vérité temporaire à ce terme. Si la valeur de vérité choisie est celle qui amène la règle à saturer, la contradiction est détectée et la déduction sur la valeur de vérité du terme peut s'effectuer : le terme inconnu prend la valeur inverse de la valeur testée, et la règle déclenchante devient invalidée. Cette manière d'effectuer des raisonnements est exactement celle que l'on nomme 'raisonnement par l'absurde'. Cependant, ceci suppose que le terme inconnu soit considéré comme pertinent par le modèle. Or, si on considère que les règles sont invisibles tant qu’elles ne sont pas saturées, on est amené à penser que cette situation ne se rencontre jamais. Ceci semble donc interdire à notre modélisation toute capacité de raisonnement logique. Cependant, si l’objectif est de déterminer la valeur de vérité d’un terme ou de démontrer qu’un terme donné prend une valeur de vérité donnée, alors la pertinence du terme en question apparaît et le raisonnement par l’absurde peut commencer.

Nous ne postulons toujours pas que les capacités logiques permettent d’émettre une hypothèse à partir de rien. La production de contre-factuel (que nous présenterons en 4.3.2) nécessite que la valeur de vérité du terme soit connue. Afin de pouvoir rendre compte de la capacité des humains à résoudre des problèmes logiques, il faut donc faire appel à l’ensemble du modèle, et notamment aux capacités opératoires de celui-ci. Nous montrerons au cours du chapitre 5 que notre modèle complet permet d’expliquer les performances humaines lors de la résolution de problèmes logiques.

4.3.1.2 Evaluation d’une situation

La détection de saturation dans le cas de la modalité indésirable permet d'évaluer une situation dans le cadre d'une résolution de problème. Il suffit pour cela de traduire en terme d'indésirabilité la négation de l'objectif poursuivi. Tant que l'objectif ne sera pas atteint, au moins une des indésirabilités restera saturée. Quand l'objectif aura été atteint, l'ensemble des indésirabilités seront cassées, et le sujet se retrouvera dans une situation non indésirable.

La traduction d'un objectif en terme d'indésirabilité se fait par l'intermédiaire d'une négation, de sorte qu'un objectif exprimé sous la forme d'une conjonction de clauses sera traduit sous la forme d'une conjonction d'indésirabilités. Ainsi, l'objectif de la tour de Hanoï, qui peut s'exprimer sous la forme "amener les disques 1, 2, 3, 4 et 5 sur le piton C" se traduira par :

[[non(disque(1,position(C)))], []] Þ Ind (1)

Ù [[non(disque(2,position(C)))], []] Þ Ind (2)

Ù [[non(disque(3,position(C)))], []] Þ Ind (3)

Ù [[non(disque(4,position(C)))], []] Þ Ind (4)

Ù [[non(disque(5,position(C)))], []] Þ Ind (5)

D'autre part, comme une situation impliquant une situation indésirable sera également considérée comme indésirable, notre modèle permet également de traduire en sous objectifs un objectif initial. Ainsi, si l'on exprime le but de la tour de Hanoï sous la forme "amener tous les disques en C", on obtiendra dans un premier temps :

[[non(disque(tous, position(C)))], []] Þ Ind

Mais comme :

[[disque(tous, position(C)), non(disque(1, position(C)))], []] Þ Faux

On en déduit :

[[non(disque(1, position(C))), []] Þ Ind (1)

Nous remarquons que la notation (Dés Þ E) n'est pas adéquate. Bien qu'elle traduise de manière plus naturelle la notion d'objectif, elle ne rentre pas dans le cadre du mécanisme simple de détection de saturation. La notation inverse (E Þ Dés) n'est pas plus adaptée car la détection de satisfaction ne s'effectuerait qu'une fois le problème résolu. En conséquence, la règle serait cassée (et donc invisible) durant toute la durée de la résolution du problème.

Il ne faudrait pas en déduire que la modalité désirable n'existe pas. Elle se manifeste notamment dans les conversations. Nous précisons seulement ici que cette modalité ne peut-être une source de motivation dans le cadre d'une résolution de problème.

La motivation d'un sujet en situation de résolution de problème est donc constituée par la suppression d'indésirabilité. En d’autres termes, la motivation d’un sujet en situation de résolution de problème est constituée par la suppression de problèmes.

4.3.2 La production de contre-factuel

Nous avons précédemment considéré la capacité des sujets à émettre des hypothèses, en envisageant les conséquences d’une situation inconnue ou en envisageant les conséquences d’une situation différente de la situation réelle. Afin de modéliser ces capacités, nous utilisons le mécanisme de production de contre-factuel. La production d’un contre-factuel consiste à inverser la valeur de vérité connue d’un terme envisagé. Nous nommerons contre-factuel un tel couple (terme, valeur de vérité hypothétique).

A titre d’exemple, au cours d’une résolution de la tour de Hanoï, si le disque 5 se trouve en A, le modèle résolvant le problème considérera que :

est_en(disque 5, position C) : Faux

Le modèle sera cependant capable d’envisager la situation où le disque 5 se trouve sur le piton C en produisant le contre-factuel :

est_en(disque 5, position C) : Vrai

Nous allons maintenant examiner les possibilités offertes par la génération de contre-factuel, tant dans la conduite d’un raisonnement qu’en tant qu’outil de planification.

4.3.2.1 La génération de contre-factuel dans le raisonnement

La génération de contre-factuel autorise l’invalidation logique directe. En effet, sans la capacité de considérer la négation de la valeur de vérité d’un terme, ce type d’invalidation serait impossible, puisque l’invalidation consiste à nier la valeur de vérité d’un des termes de la règle saturée. C’est d’ailleurs la capacité des sujets à effectuer des invalidations logiques directes qui est à l’origine de ce point de notre modélisation. Ainsi, si l'on reprend l'exemple de l'insecte :

A1 - Tiens, regarde le dard qu’elle a.

B1 - ça alors !

A2 - C’est marrant.

B2 - C’est pas un dard, c’est une trompe.

L'interlocuteur B s'étonne dans un premier temps avec A, en partageant son analyse de la situation quand à l'improbabilité qu'un insecte possède un dard aussi long, puis contre-factualise le fait que l'appendice désigné soit un dard.

La génération de contre-factuel pourrait aussi apparaître comme un moyen d’effectuer des raisonnements par l’absurde, en donnant une valeur de vérité temporaire au terme dont la valeur de vérité est inconnue dans une règle déclenchante. Cependant, nous n’autorisons pas notre modélisation à envisager spontanément une valeur de vérité pour un terme inconnu. La production de contre-factuel ne permet pas d’émettre une hypothèse pour un terme dont la valeur de vérité est inconnue, mais seulement d’envisager la négation d’un terme connu. En effet, ajouter cette hypothèse à notre modélisation ne nous permet d’expliquer rien de plus au comportement des sujets. Nous la supprimons donc dans un souci de parcimonie.

4.3.2.2 La génération de contre-factuel comme outil de planification

La génération de contre-factuel autorise aussi des capacités de planification dans une situation de résolution de problème. Nous appelons objectif courant l’objectif que le modèle est en train de poursuivre (l’objectif initial en début de résolution puis, généralement, le dernier sous objectifs calculés non encore résolu). Le principe de la planification est de construire des sous-buts à partir de l’objectif courant.

Pour réaliser cela, le modèle va construire un contre-factuel à partir de la règle d’indésirabilité saturée représentant l’objectif courant. Ce contre-factuel peut alors saturer des règles précédemment invalidées, ce qui va mener à la production de nouveaux contre-factuels par invalidation logique directe. Une fois la production de contre-factuels terminée, la nouvelle situation produite, que nous nommerons situation contre-factuelle, est cohérente et désirable[13].

La situation contre-factuelle permet alors de produire un sous-objectif par le biais d’une interaction avec les opérateurs. Nous examinerons dans le détail la génération de sous-but au cours du chapitre 6 consacré au couplage de la logique et de l’opérateur.

4.4 Les capacités d’apprentissage du modèle

Nous venons de présenter la représentation des connaissances et les mécanismes de fonctionnement de la partie logique de notre modélisation. Nous allons maintenant spécifier les lieux possibles de l’apprentissage dans cette même partie logique. Nous nous bornerons pour l’instant à préciser l’ensemble des lieux où un mécanisme d’apprentissage peut apparaître, sans prendre de décision quant à l’intégration de ce mécanisme dans notre modèle.

Deux types d’apprentissage sont possibles dans la partie logique de notre modèle. Le premier type d’apprentissage est lié à la découverte d’une incohérence entre expérience et représentation du monde. Ce type d’apprentissage se produit à chaque fois qu’une incohérence est constatée. Le second type d’apprentissage est lié au perfectionnement de la compréhension du domaine de travail : au cours d’un raisonnement, on se rend compte de la validité d’une règle donnée, puis on la mémorise. On crée alors une nouvelle règle à partir d’anciennes. Nous appellerons ce mécanisme la «compilation logique des connaissances» (qu’il convient de ne pas confondre avec le mécanisme de compilation des connaissances d’Anderson [AND 83]).

4.4.1 Apprentissage à l’épreuve des faits (incohérence constatée)

Une détection de situation paradoxale ou improbable amène toujours le sujet qui l’opère à réviser ses connaissances. Une détection de situation indésirable amène le sujet soit à réviser ses connaissances, soit à supprimer cette indésirabilité en agissant sur sa source. La suppression de la source d’une indésirabilité peut être considérée comme une résolution de problème et nous ne l’aborderons pas avant le chapitre 6. La révision des connaissances du sujet consiste soit en une simple révision factuelle, soit en une modification des conceptions du sujet (i.e. en une modification de règle).

4.4.1.1 Modification d’une connaissance factuelle

Il s’agit du cas de l’invalidation logique directe. Le modèle détecte une problématique puis se rend compte que son évaluation de la valeur de vérité d’un des éléments de cette problématique est erronée. La correction de cette évaluation suffit à résoudre la problématique. Il ne s’agit a priori pas d’un apprentissage. Cependant, si le terme remis en cause est contenu dans une règle paradoxale à terme unique, cette modification n’est plus seulement une modification factuelle, et l’on se retrouve dans le cas d’une modification de règle. Ce sera le cas à chaque fois que le modèle sera amené à modifier une connaissance ‘encyclopédique’.

4.4.1.2 Modification d’une règle

Il existe a priori deux manières de modifier une règle à l’issue d’une situation paradoxale, selon que la partie de la règle visée est le noyau ou le menu.

L’apprentissage par le noyau signifie que la règle utilisée est erronée. Les modifications possibles[14] sont la suppression de la règle, la négation de la valeur de vérité d’un de ses termes, sa spécification ou sa généralisation. Spécifier une règle consiste à la rendre applicable dans de plus rares cas. Cela revient à rajouter un terme à la règle. Généraliser une règle reviendrait à supprimer un terme. Cependant, il n’est pas nécessaire de supprimer la règle plus spécifique quand on procède à une généralisation, comme nous le verrons au paragraphe 4.4.2 consacré à la compilation des connaissances logiques.

Le premier cas d’apprentissage par le menu concerne l’invalidation logique indirecte. Une manière de voir les choses est de considérer que le modèle apprend une exception à une règle connue. Il convient toutefois de ne pas confondre cette situation avec celle où la règle correcte est connue, mais ou l’élément invalidant est mal (ou pas) évalué. A titre d’exemple, si l’on modélise la connaissance du sujet C dans la discussion sur les files d’attente, on obtient en début de discussion :

[[emmener(voiture, continent, ferry)], []] Þ IND

puis, après l’invalidation D8, on obtient :

[[emmener(voiture, continent, ferry)], [non avoir_reserve(ferry)]] Þ IND

Un deuxième type d’apprentissage consiste en la mémorisation du caractère exceptionnel d’un élément du noyau d’une règle. Dans ce cas, le noyau de la règle devient plus général (comportant moins de terme, il sature plus souvent), et le menu s’enrichit de l’élément en question.

Il est même possible de modifier une règle sans qu’une invalidation logique ait eu lieu. En effet, d’après 4.3.3.3, si la négation d’un des termes du noyau d’une règle est apprise comme improbable, l’élément en question quitte le noyau et rentre dans le menu, comme dans :

Modèle sans menu Modèle avec menu

(A, B, C) Þ Faux [[A, B, C], []] Þ Faux

(non C) Þ Improbable [[A, B], [[C]]] Þ Faux

Réciproquement, il est possible de supprimer un élément du menu pour l’intégrer dans le noyau (quand une situation se révèle plus fréquente qu’initialement estimée). Dans la notation sans utilisation du menu, cela revient à supprimer la règle indiquant que le fait n’est pas improbable. Là encore, il est donc possible d’assister à une modification de la règle sans qu’une invalidation logique ait eu lieu.

Il pourrait sembler que les deux modèles que nous avons présentés (noyau-menu et improbabilité) se comportent différemment au moment de l’apprentissage. De fait, le seul cas ou une différence apparaît est quand la valeur de probabilité a priori d’un terme est modifiée suffisamment pour que ce terme passe du noyau au menu ou réciproquement. Mais comme nous ne nous intéressons pas aux valeurs de probabilité, cette différence ne se fera pas sentir pour nous.

4.4.2 Compilation logique des connaissances

Notre modèle permet de proposer un mécanisme d’apprentissage qui n’est pas basé sur les invalidations. Nous appelons ce mécanisme compilation logique des connaissances, car il permet de créer de nouvelles règles logiques à partir d’anciennes. Ce mécanisme peut également être vu comme un processus de compréhension : les règles et les contraintes déjà connues induisent d’autres règles et contraintes. Ce mécanisme ne nécessite pas de supposer une capacité «d’oubli» des règles utilisées pour la compilation, car les règles compilées masquent quand c’est nécessaire les règles plus anciennes. La remise en cause temporaire d’une règle compilée permet même alors de fournir sa démonstration.

4.4.2.1 Principe de la compilation

Quand, en situation de raisonnement ou plus généralement en situation de résolution de problème, une situation problématique est détectée, il est possible de créer une règle constituée de la conjonction de l’ensemble des termes dont la valeur était connue avant la détection, à l’exclusion des contre-factuels. Considérons :

[[A, B], []] Þ Indésirable (1)

[[non A, C], []] Þ Indésirable (2)

(B : vrai) (3)

(C : vrai) (4)

Les règles (1) et (2) n’étant pas saturées, aucune problématique n’est détectée. Si dans cette situation, A est envisagé (par production de contre-factuel à l’issue d’un blocage, comme nous le verrons en 6.3.2), la règle (1) sature. Le mécanisme de génération de contre-factuel détruit alors A et produit non A. La règle (2) sature à son tour. Le mécanisme de production de contre-factuel échoue alors (en supposant que seuls A, B et C soient pertinents pour le problème en question) et la situation indésirable est détectée. Il est alors possible de créer une nouvelle règle à partir des faits tenus pour vrai au début de la production des contre-factuels. Cette nouvelle règle comportera :

· La modalité détectée.

· Un noyau composé de la conjonction des termes ayant une valeur de vérité connue au début de la production contre-factuelle et apparaissant dans le noyau des règles ayant servi lors de la compilation. Chacun de ces termes apparaîtra dans le noyau avec la valeur de vérité qu’il avait au début de la production contre-factuelle.

· Un menu composé de l’union des termes apparaissant dans les menus des règles ayant servies lors de la compilation, et dont la valeur de vérité était connue au début de la production contre-factuelle. Là encore, chacun de ces termes apparaîtra dans le menu avec la valeur de vérité qu’il avait au début de la production contre-factuelle.

Dans l’exemple que nous venons de traiter, cela donne :

[[B, C], []] Þ Indésirable (6)

Ce mécanisme ne nécessite pas que les règles puissent déclencher. La détection de saturation est suffisante pour permettre la compilation. Si l’on se borne à supposer la détection de saturation, la compilation ne se déclenchera au plus tôt qu’à la première manifestation du problème (dans notre exemple, à la production du contre-factuel sur A). Si l’on postule la possibilité pour les règles de déclencher, alors la compilation prend place dès que les règles sont connues. Cette seconde hypothèse n’est pas compatible avec les performances des sujets humains placés en situation de résolution de problèmes logiques, car dans ce cas la performance devient automatiquement parfaite. Elle est donc rejetée. Nous reviendrons sur le mécanisme de compilation des connaissances au cours du chapitre 6, après avoir présenté dans le détail le rôle de la production de contre-factuel dans la résolution de problème.

La justification de la manière de placer les termes dans le menu ou dans le noyau est la suivante : le modèle démontre une nouvelle règle qui sera vraie de manière certaine quand les termes invalidant les règles utilisés pour effectuer cette démonstration n’auront pas la valeur de vérité invalidante. Ainsi, les exceptions aux règles permettant la démonstration seront aussi des exceptions pour la règle en question. On notera aussi que les termes des menus dont la valeur de vérité n’est pas connue au début de la production contre-factuelle n’interviennent pas dans la nouvelle règle, car les prendre en compte obligerait à postuler l’exploration systématique des règles étant intervenues dans la démonstration. Le mécanisme de compilation logique peut donc ‘surgénéraliser’, en apprenant des règles ayant un menu incomplet.

Enfin, la compilation logique des connaissances aboutit bien au même résultat dans le modèle à modalité improbable, comme l’illustre l’exemple suivant (SI désigne la situation initiale, CF marque le début de la production contre-factuelle et CC désigne la conclusion de la compilation logique) :

Modèle sans menu Modèle avec menu

SI : (C : vrai) (C : vrai)

(B : vrai) (B : vrai)

(E : faux) (E : faux)

(A, B, C) Þ Faux [[A, B], [C]] Þ Faux (1)

(non C) Þ Improbable

(non A, non E, D) Þ Faux [[non A, non E], [[D]]] Þ Faux (2)

(non D) Þ Improbable

CF : (A : vrai) (A : vrai)

(1) saturé (1) saturé

(A : Faux) (A : Faux)

(2) saturé (si D ignoré) (2) saturé

CC : (B, C, non E) Þ Faux [[B, non E], [C]] Þ Faux

La conclusion sur le modèle improbable est bien la même que sur le modèle noyau-menu, puisque la règle (non C) Þ Improbable donne bien à C le statut de terme ‘oubliable’ dans la règle (B, C, non E) Þ Faux.

4.4.2.2 La compilation en tant que mécanisme de compréhension

Il est possible de voir la compilation comme un mécanisme de compréhension. Le sujet se trouve dans une situation problématique, constate que la problématique provient de la conjonction d’un ensemble de termes donnés, et mémorise cette conjonction. Le sujet a donc ‘compris’ que la conjonction des termes donnés posait problème. Et on peut même prétendre qu’il a compris pourquoi, puisqu’il pourra évoquer comme explication les règles (et les contre-factuels) qui lui ont permis de générer cette nouvelle règle.

Prétendre que le sujet à compris, c’est supposer qu’il est capable d’expliquer. Nous allons maintenant voir comment cette compréhension peut permettre, dans une certaine mesure, de retrouver la démonstration, et donc l’explication, de la règle compilée.

4.4.2.3 Le «masquage» des anciennes règles

Lorsqu’une nouvelle règle est apprise se pose la question du devenir des règles précédentes. On peut ainsi se trouver dans une situation où la règle compilée est une généralisation d’une règle précédemment connue, comme dans l’exemple :

[[A, B, C], []] Þ Faux (1)

[[non C], []] Þ Faux (2)

La compilation peut générer la règle :

[[A, B], []] Þ Faux (3)

La règle (1) est maintenant inutile, puisque à chaque fois qu’elle se déclenche, la règle (3) se déclenche (alors que la réciproque est fausse, (1) nécessitant en outre de connaître la valeur de vérité de C, ce qui n’est pas le cas pour (3)).

Nous ne postulons cependant pas qu’un mécanisme d’oubli vienne actualiser les connaissances du sujet en supprimant les règles inutiles dans une telle situation. Une règle plus générale masque simplement les règles qui lui sont spécifiques. Le maintien des règles spécifiques autorise même un mécanisme d’explication. Si la règle compilée est remise en cause (i.e. temporairement supprimée), les règles ayant permis de la construire redeviennent apparentes. Si le sujet est capable d’envisager les contre-factuels adéquats, il pourra alors démontrer la validité de la règle compilée.

Cette capacité d’explication peut rencontrer deux limites. La première provient du fait que le sujet ne sera pas nécessairement capable d’envisager correctement le bon contre-factuel[15]. La seconde limite provient du fait que le sujet a pu apprendre de nouvelles règles depuis la compilation de la règle à expliquer. Dans ce cas, envisager le contre-factuel ayant permis la compilation risque de ne pas suffire à expliquer la règle car l’échec sur la production de contre-factuel risque de survenir trop tôt, comme dans l’exemple :

[[A, B, D], []] Þ Faux (1)

[[non A, C, D], []] Þ Faux (2)

Quand B, C et D sont vrais, et en produisant le contre-factuel A (ou non A), on déduit :

[[B, C, D], []] Þ Faux (3)

Si par la suite, on mémorise la règle :

[[A, C], []] Þ Faux (4)

Il devient alors impossible de démontrer la règle (3) en produisant un contre-factuel sur A car (4) sature pour A vrai, et (2) sature pour A faux. La règle (3) est bien sûr toujours valide, mais il est impossible de la démontrer sans masquer la règle (4). De fait, il est toujours possible de démontrer soit la règle que l’on désire démontrer, soit une règle plus générale. Ainsi, dans l’exemple proposé, le mécanisme de compilation peut produire la règle plus générale (B Ù D) Þ Faux.

4.5 Synthèse du modèle

Nous sommes maintenant en mesure de présenter une synthèse de la partie logique de notre modèle, en indiquant d’abord la représentation des connaissances choisies, puis en rappelant l’ensemble des mécanismes que nous postulons.

4.5.1 Représentation des connaissances

La représentation des connaissances se divise en une représentation des connaissances à long terme du sujet, sous forme de règles, et une mémoire de travail où seront stockés les faits et les contre-factuels qu’il envisage au cours de la résolution.

4.5.1.1 Les règles

Une règle représente une connaissance à long terme du sujet. Elle décrit une situation problématique (dont la modalité est précisée) par le biais d’un noyau. Cette règle peut être accompagnée d’exceptions qui sont stockées dans un menu.

Une règle indique que la conjonction d’un ensemble de termes est problématique. Le type de problématique est appelé modalité. Nous utilisons deux modalités :

· La modalité Incompatible qui indique que la conjonction des termes présents dans la règle est impossible.

· La modalité Indésirable qui indique que la conjonction des termes présents dans la règle est indésirable.

L’étude ayant amené cette modélisation fait apparaître une troisième modalité (la modalité Improbable), que nous ne reprenons pas dans cette modélisation car elle n’apparaît jamais nécessaire pour expliquer le comportement d’un sujet en situation de résolution de problème.

Une règle se divise en un noyau et un menu. Le noyau est constitué d’une conjonction de termes. Le menu est une liste d’exceptions, chaque exception prenant la forme d’une conjonction de termes. La sémantique d’une règle est donc que la conjonction des termes du noyau est indésirable ou incompatible (en fonction de la modalité), sauf quand un des éléments du menu n’est pas vérifié. Une règle prend donc la forme :

[Menu, Noyau] Þ Modalité

Dans la notation précédente Menu prend la forme d’une conjonction de termes, Noyau prend la forme d’une liste de conjonctions de termes et Modalité prend sa valeur dans {Indésirable, Incompatible}.

4.5.1.2 Les faits

Les connaissances à court terme (ou faits) sont stockées sans ordre particulier, sous la forme :

Fait : Valeur de vérité <CF>

Dans la notation précédente, Fait désigne l’énoncé du fait et Valeur de vérité sa valeur de vérité actuellement associée. CF n’apparaît que si le fait concerné est un contre-factuel.

Un contre-factuel est un fait dont le sujet sait que la valeur de vérité est l’inverse de celle qu’il lui attribue temporairement.

4.5.2 Mécanismes de fonctionnement

Notre modèle dispose de trois mécanismes pour agir sur les connaissances logiques. La saturation d’une règle entraîne la détection d’une situation problématique. La production de contre-factuel permet de sortir d’une telle situation. Enfin, la compilation des connaissances offre un mécanisme d'apprentissage de nouvelles règles et offre des capacités limitées d'explication.

4.5.2.1 Détection par saturation

On dit qu’une règle est saturée quand chacun des termes présent dans la règle est connu comme vrai. On dit qu'une règle est cassée quand au moins un des termes présent dans la règle est connu comme faux. La première capacité que nous prêtons à notre modèle est la détection systématique des saturations. Lorsque le noyau d'une règle est saturé, et que son menu n'est pas cassé, la modalité correspondante est détectée. Lorsqu'une règle n'est pas saturée ou lorsqu'elle est cassée, la règle est invisible.

4.5.2.2 Déblocage par contre-factuel

Afin de sortir d'une situation problématique, aussi appelée impasse, le module logique peut produire des contre-factuels. La production de contre-factuel consiste à inverser la valeur de vérité d'un terme connu.

On peut voir la production de contre-factuel comme un moyen d'émettre des hypothèses ou comme un moyen d'envisager les prérequis pour résoudre une situation problématique. La production de contre-factuel autorise les invalidations logiques, et permet de se fixer des sous-objectifs en situation de résolution de problème comme nous le verrons au paragraphe 6.3.2.

4.5.2.3 Compilation logique des connaissances

La troisième capacité que nous prêtons à notre modèle est la capacité de compilation logique des connaissances. La compilation consiste à mémoriser comme règle la conjonction des faits connus (à l’exclusion des contre-factuels) quand une problématique est détectée. La règle ainsi créée portera la modalité détectée. La compilation logique des connaissances permet d'apprendre de nouvelles règles et, dans une certaine mesure, de fournir la justification de ces nouvelles règles.

précédent

Retour au Plan

suivant

© Copyright Jean-Bernard AURIOL

C.V. de Jean-Bernard Auriol

dernière mise à jour le

25 Janvier 2002

---

[1] Si la situation présentée est désirable, la conversation s’arrête par un co-réjouissement (bien qu’un interlocuteur un peu sadique puisse être tenté de banaliser, d’invalider ou ‘d’antagoniser’ la réplique).

[2] Le premier locuteur doit remettre en question sa perception de la situation qu’il évoque mais pas la conception qu’il se fait du monde puisqu’une fois l’invalidation directe effectuée la problématique s’effondre. Bien entendu, si le terme nié par le second interlocuteur est considéré comme un fait certain par le premier, celui-ci peut-être amené à modifier cette croyance, et donc sa conception du monde.

[3] C5 - Je veux dire qu’emporter une voiture sur le continent, c’est l’enfer.
A6 - non.
C9 - Et bien, je vous parle de ce que j’ai entendu, je veux dire chaque été, on voit des histoires de
queues fantastiques à…
D8 - mais il s’agit de gens qui n’ont pas réservé.

[4] La dénomination ‘atténuation’ n’est pas utilisée par J.-L. Dessalles dans les travaux que nous présentons ici. Nous l’introduisons cependant pour regrouper les deux types d’invalidations ayant trait à une modification de la position des répliques dans l’espace désirabilité*probabilité.

[5] Nous avons vu précédemment qu’il n’était pas toujours aisé de décider si une première réplique était sur le mode indésirable ou improbable. Il existe même des cas où l’on peut considérer la première réplique comme étant bimodale. Mais l’antagonisation, par sa structure, ne peut déplacer la réplique à invalider que sur l’axe de l’indésirabilité. C’est en cela qu’elle ne s’applique que pour la modalité indésirable.

[6] A ceci près que, dans notre cadre, toutes les variables sont universellement quantifiées.

[7] De fait, il faudrait représenter les règles d’indésirabilité en précisant la valeur d’indésirabilité associée. Mais cette représentation simplifiée est suffisante dans la totalité des travaux présentés dans ce manuscrit. Nous nous limiterons donc à cette représentation dans la suite de ce document.

[8] Dire que les règles sont communes revient à dire qu’elles ne sont pas communiquées : le second interlocuteur les connaissait déjà. Le premier intervenant apporte seulement les valeurs de vérité des termes intervenant dans le contexte et la conséquence de ce terme (ici, l’indésirabilité).

[9] C’est le sens de l’intervention A6 dans l’exemple du Ferry en 4.1.2.1.2.

[10] (2’b) ne signifie pas qu’il est improbable qu’un fléchage ne soit pas écrit en Français dans une situation donnée, mais plutôt que A n’a pas l’habitude de voir des fléchages dans une langue étrangère.

[11] Ou une (in)désirabilité…

[12] Nous utiliserons des menus nuls (i.e. ne proposant aucune invalidation logique indirecte) chaque fois que la présence d’un élément dans le menu ne sera pas indispensable, et ce afin de faciliter la lecture de ce document.

[13] Si l’on considère qu’en situation de résolution de problème, les sujets ne poursuivent qu’un objectif à la fois. Sinon, la situation peut être encore indésirable (cas où plusieurs objectifs ne sont pas atteints), mais elle l’est moins puisque au moins une des règles d’indésirabilité a été invalidée.

[14] Rappelons que nous nous bornons ici à faire l’état des lieux d’apprentissage compte tenu du modèle. Les apprentissages que nous proposons peuvent apparaître compte tenu de notre modélisation, mais ne résultent pas de l’analyse de comportement de sujets humains. La question de savoir si une règle peut effectivement être supprimée, par exemple, n’est pas pour nous tranchée. Reste qu’au sein du modèle, rien n’interdit la suppression d’une règle. C’est en ce sens que cette modification est ‘possible’.

[15] Comme nous le verrons plus tard, la production de contre-factuel se déclenche à l’occasion d’un blocage. Un sujet interrogé sur la validité d’une règle ne sera pas nécessairement capable de produire le contre-factuel permettant la compilation.