L’Opération de Hilbert

(d’après le Cours d’Algèbre de Roger Godement, Hermann, Paris, 1936, pp.38 ssq.)

Dans le système de N. Bourbaki ( Eléments de Mathématique) , on utilise sept signes fondamentaux, et des lettres.

 Quatre signes fondamentaux que voici

ou, non, ,

sont de nature purement logique; les trois autres sont de nature mathématique à proprement parler, ce sont les signes

=, , ,

Un assemblage s'obtient en écrivant une succession de signes et de lettres, certains des signes  figurant dans un assemblage pouvant de plus être joints à certains des signes   par des liens  ^___  ; par exemple, l'expression

est un assemblage.

 

Soit A un assemblage, et soit x une lettre; nous allons indiquer un procédé pour en déduire un nouvel assemblage qui ne contient plus la lettre x mais que l'on désigne néanmoins par la notation _.

On l'obtient en effectuant les trois opérations suivantes

a)     on écrit l'assemblage A obtenu en faisant précéder l'assemblage A du signe

b)    on joint le signe   placé devant A à chaque occurrence de la lettre x par un lien;

c)     dans l'assemblage obtenu, on remplace partout la lettre x par le signe . Si par exemple A est l'assemblage écrit plus haut, alors  est l'assemblage

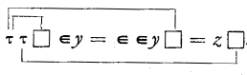
L'opération faisant passer de A à est essentiellement due à Hilbert; on en donnera plus loin la signification intuitive.

Nous allons maintenant énoncer les critères de formation des objets et des relations mathématiques; les voici

Objets :

-         (OM I) : Toute lettre est un objet mathématique.

-         (OM 2) : Si A et B sont des objets mathématiques, l'assemblage AB, qu'on désigne pratiquement par (A, B), est un objet mathématique.

-         (OM 3) : Soient A et T des objets mathématiques, x une lettre; alors l'assemblage (Alx)T déduit de T en y remplaçant partout la lettre x par l'assemblage A, est un objet mathématique.

-         (OM 4) : Soient R une relation et x une lettre. Alors l'assemblage  est un objet mathé­matique.

Relations :

-         (R I) : Si R et S sont des relations, l'assemblage {ou RS}, qu'on écrit pratiquement (R ou S), est une relation.

-         (R 2) : Si R est une relation, l'assemblage {non R} est une relation.

-         (R 3) : Soient R une relation, x une lettre, et A un objet mathématique. L'assemblage (Alx)R est une relation.

-         (R 4) : Soient A et B des objets mathématiques. L'assemblage { = AB }, qu'on écrit pratiquement A = B, est une relation.

-         (R 5) : Soient A et B des objets mathématiques. L'assemblage { AB}, qu'on écrit pratiquement {A B}, est une relation.

Il n'y a pas d'autres méthodes, en Mathématiques, pour former des objets mathématiques et des relations; et, à l'exception de (OM4), qui ne s'utilise presque jamais directement, tous les critères précédents sont effectivement utilisés à chaque instant dans la pratique.

On remarquera que les quantificateurs  et  et n'interviennent pas dans ce qui précède : c'est parce qu'on va maintenant pouvoir (en utilisant l'opération de Hilbert) les introduire comme simples abréviations.

De façon précise, soient R une relation et x une lettre; alors

sera, par définition, la relation

qu'on déduit de R en y remplaçant partout la lettre x par l'objet mathématique . Par suite, pour que la relation soit vraie, il faut et il suffit que l'objet  vérifie la relation R, et ceci conduit à l'interprétation intuitive de l'opération de Hilbert: celle‑ci consiste à choisir une fois pour toutes, pour chaque relation R et chaque lettre x, un objet vérifiant la relation R {x} (s'il en « existe »; dans le cas contraire est un objet dont on ne peut rien dire). Il va de soi que ce « choix » est purement fictif : l'intérêt de l'opération de Hilbert est de donner un procédé parfaitement

artificiel mais purement mécanique pour construire effectivement un objet dont on sait seulement qu'il satisfait à des conditions imposées d'avance (dans le cas où de tels objets existeraient). On l'utilise aussi maintenant à la place de l'axiome du choix.

Dans la pratique courante, il est tout à fait exceptionnel d'avoir à utiliser l'opération de Hilbert qui ne peut évidemment conduire à aucun résultat « explicite ». Comme le Dieu des philosophes, l'opération de Hilbert est incompréhensible et ne se voit pas; mais elle gouverne tout, et ses manifestations sensibles éclatent partout.