PRINCIPES
DU TRAITEMENT DES SIGNAUX SONORES
Pr Léo Thourel et Pr Bernard Thourel
3 -Décomposition d'un signal périodique en
fréquences
Série de Fourier:
Considérons maintenant un signal électrique correspondant à
un son. Très généralement ce signal est périodique, c'est-à-dire
qu'il se renouvelle identique à lui-même toutes les durées T
dans le temps. T
est alors appelé la période du signal : la figure 4a montre un tel signal,
en fonction du temps.
Le signal est périodique et de période et comporte donc nécessairement une composante de fréquence:
|
|
|
(5) |
d'après la définition de la fréquence.
Cette composante aura une certaine amplitude A
(voir figure 4b) et
pourra s'écrire d'après (1) et (5) :
|
|
|
(6) |
| |
En toute rigueur la courbe de fréquence 
devra être décalée
d'une certaine durée pour que la différence entre la courbe de la figure a et
la courbe de la figure b soit minimale, ce qui correspond à un décalage
angulaire (on dit un déphasage) 
. Il faut donc écrire (6) sous la forme
|
S |
|
(7) |
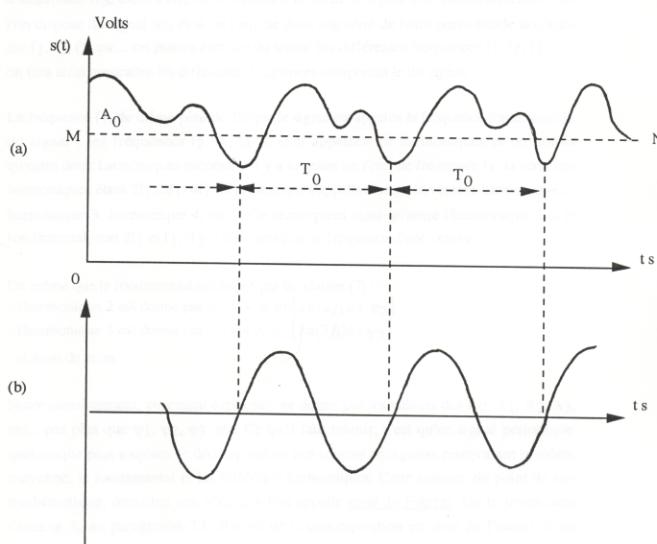
Figure 4
D'autre part la figure 4a montre
que s(t) peut osciller autour d'une valeur moyenne A
représentée par la droite MN parallèle à Ot ; pour en tenir
compte il faudra ajouter A
à (7) ce qui donne:
|
|
(8) |
Mais il n'y a pas pour autant identité entre S'
(t) et s(t) représentée par la courbe (a). On peut imaginer
d'ajouter à l'expression (8) un certain nombre de sinusoïdes de fréquences 2f
,3f
,4f
,etc.. avec des amplitudes A2, A3, A4
... et des déphasages 
... pour que la somme de tous ces signaux donne exactement
s(t). Si l'on y arrive, on sera certain qu'en ajoutant la fréquence f1,d’amplitude
A1, puis f2d'amplitude A2, puis f3
d'amplitude A3, etc... à A0, on obtiendra à la sortie le
signal s(t). Réciproquement, sil l'on dispose du signal s(t) et si on l'envoie
dans une série de filtre passe-bande accordés sur f1, f2,
f3, etc... on pourra extraire du signal les différentes fréquences f1,
f2, f3, etc... : on fera ainsi apparaître les
différentes fréquences composant le dit signal.
La fréquence f
, de même période T
que le signal est appelée la fréquence fondamentale du
signal ; les fréquences f2, f3, f4 etc... sont
appelées les harmoniques et on notera qu'entre deux harmoniques successifs il y
a toujours un écart de fréquence f
, la série des harmoniques étant 2f
, 3f
,4f
, 5f
, etc... qui s'appellent respectivement harmonique 2,
harmonique 3, harmonique 4, etc.... On remarquera aussi qu'entre l'harmonique 2
et le fondamental, soit 2f
et f
,il y a une variation de fréquence d'une octave.
De même que le fondamental est donné par la relation (7) :
-
l'harmonique 2 est donné par S
(t) = A
sin
-
l'harmonique 3 est donné par S
(t) = A
sin 
et ainsi de suite.
Notre raisonnement, purement explicatif, ne donne pas les
valeurs des 
etc... pas plus
que IP2, 
etc. Ce qu'il faut
retenir, c'est qu'un signal périodique quelconque peut toujours se décomposer
en une somme de signaux comportant la valeur moyenne, le fondamental et les
différents harmoniques. Cette somme, du point de vue mathématique, constitue
une série que l'on appelle série de Fourier. On trouvera dans l'annexe A, au
paragraphe 2 la théorie de la décomposition en série de Fourier et les formules
qui permettent de calculer 
... ainsi que 
..connaissant
l'expression de s(t) . On voit donc que le signal peut être représenté soit
dans le domaine temporel [c'est s(t) ], soit dans le domaine des fréquences, ce
qui constitue le spectre du signal. Ces deux représentations d'un même
phénomène sont équivalentes et correspondent à des choses qui existent
réellement. Suivant le traitement que l'on désire effectuer, on choisira l'un
ou l'autre. La figure 3 de l'annexe A est un exemple de spectre arrêté à
l'harmonique 6. D'une façon tout à fait générale un harmonique de rang n
s'écrira :
A
(9)
En remarquant que le sinus d'un angle est égal au cosinus de son angle complémentaire on pourra écrire, en posant:
(10)
que
(11)
et que le signal pourra se représenter indifféremment de deux façons
s(t)
= 
(12)
ou encore
:
s(t)
= 
(13)
où d'ailleurs 
peuvent être positifs
ou négatifs. Les déphasages sont toujours référés à une origine arbitraire que
l'on fixe au mieux de la complexité des formules.
Plus généralement dans le domaine indéfini des fréquences, on pourra écrire :
s(t)
= 
(14)
qui est la relation qui a été utilisée pour l'annexe A. Dans (14) les fréquences des différents harmoniques peuvent varier jusqu’à l’infini, mais les caractéristiques physiques des matériels imposent des limites. Tout amplificateur de sons constitue un filtre passe-bande et doit être capable de transmettre sans déformation tout le signal utilise s(t) : il est clair qu'il faut que la bande passante de filtre, c'est-à-dire la zone de fréquence pour lesquelles le gain de l'amplificateur reste constant, soit supérieure à la bande de fréquences occupées ras le signal, faute de quoi les signaux utiles seront déformés par le matériel.
De façon un peu plus mathématique, si H(f) est la fonction qui représente l'amplification de l'amplificateur dans le domaine des fréquences (on dit aussi la fonction de transfert du filtre équivalent) et si X(f) est la fonction qui représente le spectre du signal d'entrée, le spectre du signal de sortie Y(f) sera:
Y(f ) = H(f ).X(f) (15)
La relation (14) ne permet pas, seule, le calcul des valeurs
des A
. Il n'est pas possible d'aborder ici ce travail dont les principes
sont exposés aux paragraphes 4 et 5 de l'annexe A. En partant des relations
harmoniques établies à partir de la méthode dite des exponentielles
imaginaires, on peut montrer que la valeur moyenne de s(t) est:
(16)
et que les amplitudes des harmoniques de rang n peuvent être tirées de la relation (20) de l'annexe A à savoir:
(17)
avec 
.
 |
précédent |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
© Copyright Bernard AURIOL (email : )