Afin d’obtenir une estimation de l’audition dans la population de recrutement de la méthode, la moyenne globale des déficits auditifs dans le fichier complet a été calculée, fréquence par fréquence et en distinguant audition osseuse et aérienne.

Cette moyenne a servi de base à une catégorisation dichotomique : pour une mesure donnée (par exemple audition aérienne droite à 1500 Hz), chaque sujet a reçu une note de bonne audition : “ +1 ” si le sujet a une meilleure audition que la moyenne, et “ -1 ” si le sujet présente une audition inférieure à la moyenne.

Afin de pouvoir tester la validité de l’échelle obtenue, le fichier des questions du MMPI a été séparé en 2 parties, la première servant à établir l’échelle et la seconde servant à tester l’échelle obtenue.

Seuls les sujets ayant reçu à la fois des tests d’audiométrie et le test du MMPI ont été retenus pour les calculs. En outre, pour quelques sujets les données du test d’audiométrie préalable à l’application de la méthode n’étaient pas disponibles. Finalement, 625 sujets ont constitué le fichier de base.

afin de pouvoir tester le caractère prédictif de l’échelle sur l’efficacité de la méthode, il était nécessaire d’avoir dans les deux parties du fichier le même nombre de sujets ayant non seulement passé une première fois MMPI et tests d’audiométrie, mais aussi le même nombre de sujets ayant ensuite reçu des séances d’oreille électronique.

Parmi les 625 sélectionnés, nous avons donc séparé les 202 sujets ayant reçu la cure des 423 qui n’avaient reçu que les tests initiaux (MMPI et audiométrie). Pour ce faire, nous avons attribué un code “ cure ” à chaque sujet, selon qu’il avait reçu des séances d’oreille électronique (1) ou seulement passé les tests (0).

Sur chacun de ces fichiers, nous avons pratiqué une dichotomie aléatoire, afin d’obtenir un fichier de calcul et un fichier de test de l’échelle obtenue. Le principe de la dichotomie était le suivant : chaque sujet reçoit automatiquement un numéro séquentiel lors de la passation des tests. Nous avons donc ordonné les sujets par leur numéro. Ensuite nous avons attribué alternativement un code filtre “ 0 ” ou “ 1 ”. Cette façon de procéder permet en outre d’éliminer d’éventuels biais liés à la période de passation des tests puisque les deux fichiers contiennent le même nombre de sujets ayant passé les tests à la même période.

Finalement le fichier de calcul se compose de 101 sujets ayant reçu cure et tests, et de 212 sujets n’ayant reçu que les tests (n= 313). Le fichier de vérification se compose de 101 sujets ayant reçu cure et tests, et de 211 sujets n’ayant reçu que les tests (n = 312).

Afin de déterminer quelles questions étaient susceptibles de s’intégrer dans l’échelle Au, l’hypothèse de travail que nous avons adoptée était que la présence de réponses atypiques devaient être corrélée avec des déficits tandis que la présence de réponses typiques devait être corrélée avec une audition au moins aussi bonne que la moyenne. En fait, comme nous le verrons, il s’est avéré que pour une petite minorité de questions, la corrélation était significative mais dans le sens contraire à ce que nous attendions, à savoir que les réponses atypiques allaient avec une meilleure audition et les réponses typiques avec une audition détériorée.

Nous avons procédé à un calcul extensif des corrélations entre la présence d’une déficience auditive (mesurée par un déficit auditif supérieur à la moyenne du fichier) et le caractère typique ou atypique des réponses des sujets aux questions du MMPI. Étant donné qu’il y a 38 variables audiométriques (11 mesures pour l’audition aérienne et pour chaque oreille, 8 mesures pour l’audition osseuse et pour chaque oreille), croisées avec 550 questions, 20900 tests de Chi-2 ont donc été pratiqués au moyen du logiciel SPSS.

Tous les résultats significatifs au seuil de p = .02 ont ensuite été extraits.

Dans un premier temps nous avions pensé simplement retenir les questions dont la contribution était significative avec le plus grand nombre de variables. Ainsi une question significativement corrélée avec 25 seuils auditifs (sur 38) était mieux classée qu’une variable corrélée avec seulement 15 seuils.

Il est cependant apparu qu’un petit nombre de questions pouvaient avoir une contribution significative positive avec certaines fréquences et négatives avec d’autres. Nous avons donc décider d’appeler questions alignées celles pour lesquelles une réponse typique était corrélée avec une bonne audition et questions contre-alignées les questions telles qu’une réponse typique est corrélée avec une mauvaise audition. Pour la grande majorité des questions ayant une corrélation avec un grand nombre de variables, nous avons pu constater que la plupart du temps une même question était soit alignée soit contre-alignée avec l’ensemble des variables mesurées. Ce phénomène implique que la contribution de ces questions n’est pas due au hasard car celui-ci aurait produit une répartition relativement symétrique, c’est à dire avec à peu près autant de contributions positives que de contributions négatives.

Néanmoins, afin de nous prémunir contre les difficultés d’interprétation potentielles des questions alignées avec certaines variables et contre-alignées avec d’autres, nous avons préféré opérer un classement des questions basé sur la valeur absolue de la différence entre le nombre de variables alignées et le nombre de variables non alignées. Ainsi une question corrélée avec 25 seuils auditifs sur 38 mais dont 20 étaient alignés et 5 contre alignés recevait une valeur de classement de 20 – 5 = 15. Elle était donc moins bien classée qu’une question corrélée avec 20 seuils mais tous alignés.

Finalement, nous avons retenu les 50 questions les mieux classées. Ces questions sont exposées en annexe 1.

Généralement les échelles du MMPI se présentent sous forme de notes T qui sont des valeurs normalisées (moyenne 50 écart-type 10). Afin de respecter ces conventions largement admises, nous avons nous même procédé à une normalisation en notes T.

Les paramètres de base de cette normalisation (moyenne et écart type) ont été établis à partir du fichier de calcul, c’est à dire à partir de la partie du fichier retenue pour l’élaboration de l’échelle (n = 313), sans tenir compte du fichier de vérification, c’est à dire de la partir du fichier global destinée à tester la validité de l’échelle obtenue.

Le total des points se calcule à partir du nombre de questions contributives pour lesquels le sujet a répondu de façon atypique.

Dans le présent cas, nous avons vu que l’échelle Au contenait un certain nombre de questions contre-alignées, c’est-à-dire que c’est le caractère typique de la réponse qui contribue à un mauvais pronostic.

Le principe du calcul est donc le suivant : on examine les réponses du sujet sur les questions qui constituent l’échelle. On compte un point quand le sujet a répondu de façon typique a une question contre-alignée ou s’il a répondu de façon atypique a une question alignée. Dans les autres cas, on ne compte aucun point. Le récapitulatif des questions qui constitue l’échelle, (annexe 1) indique directement quelle réponse du sujet donne lieu à l’attribution d’un point.

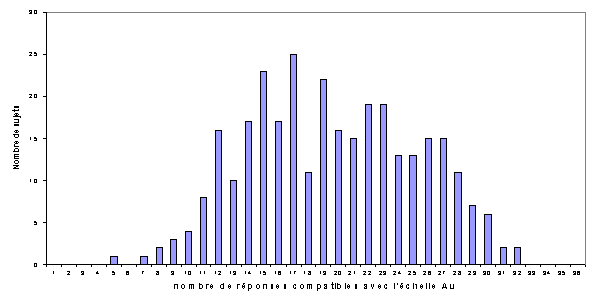
Figure 25 : distribution des sujets selon le nombre de réponses à l’échelle Au
(déterminée sur le fichier de calcul, n = 313)

La distribution des totaux obtenue sur les 313 sujets de notre fichier de calcul a fournit les résultats suivants :

On voit que la distribution est normale. La moyenne est 18,6 et l’écart type est 5,6.

On obtient donc facilement la note T pour un sujet donné en appliquant la formule suivante

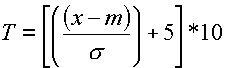
où x est le total de point obtenu par le sujet

                m = 18,6

                s = 5,55

Néanmoins, afin de faciliter l’utilisation de l’échelle, un tableau de conversion est proposé en annexe 2. Ce tableau donne directement la note T associée à un total donné.

Une fois obtenu le mode de calcul de l’échelle, nous avons pu passer à la seconde phase, à savoir le test de la capacité prédictive de l’échelle.

Nous sommes partis cette fois de la seconde partie du fichier, c’est à dire des données relatives aux 312 sujets sélectionnés aléatoirement comme il est décrit plus haut.

Nous avons commencé par calculer le total des points obtenus sur l’échelle Au pour chacun des 312 sujets. Nous avons ensuite obtenu la note T en appliquant la formule de calcul énoncée précédemment.

La question qui se posait alors était :est-ce que l’échelle permet de fournir une prédiction sur les gains réalisés grâce à la cure d’oreille électronique ?

Pour tester cette hypothèse, nous avons commencé par sélectionner les données relatives aux 101 sujets du fichier de vérification ayant passé le test de MMPI et ayant ensuite reçu des séances d’oreille électronique.

Nous avons alors calculé pour chaque ligne de ce fichier les gains relatifs, par fréquence. Du fait que les études préliminaires ont montré que les abaissement de seuil qui résultent de l’oreille électronique suivent une fonction exponentielle décroissante du nombre de séances, nous avons commencé par calculer un gain relatif au nombre de séances, puis nous avons passé cette mesure en logarithme népérien.

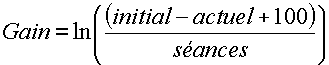
Les variables “ actuel ” et “ initial ” sont les seuils auditifs respectivement mesurés au moment du test auquel correspond la ligne et au moment du test initial. L’opération est dans le sens initial – actuel car les valeurs mesurées sont des déficits. Un gain correspond donc à une réduction du déficit et donc à une valeur après la cure inférieure à la valeur d’avant la cure. La variable “ Séances ” est le nombre de séances d’oreille électronique reçues par le sujet au moment du test.

Nous avons donc ensuite calculé le modèle de régression linéaire entre l’échelle Au et les gains tels que calculés par la formule précédente.

Les résultats sont probants puisque la régression est significative pour toutes les fréquences et dans toutes les conditions.

Le tableau suivant est extrait des résultats de régression obtenus par le logiciel SPSS. On remarque que le coefficient de la pente de régression, b1, est toujours négatif, ce qui était prévisible. L’interprétation est que plus la note obtenue sur l’échelle Au est faible, et plus élevés seront les gains. On remarque aussi la force de la relation puisque pour toutes les fréquences considérées, que ce soit en audition aérienne ou osseuse, le risque est toujours inférieur ou égal à p = .001. Seule la fréquence de 500 Hz en audition osseuse gauche (GSOG2) a un seuil de p = .002 ce qui reste très acceptable, surtout si l’on tient compte de l’homogénéité de ces résultats.

Tableau 5 : Paramètres des équations de régression (et seuils de signification)
de l’échelle “ Au ” sur les gains apportés par la cure d’oreille électronique.

Rappel : b0 et b1 représentent respectivement l’intercept et la pente de la courbe de régression. Ainsi ces résultats suggèrent que le gain relatif au nombre de séances varie comme une fonction inverse de la note sur l’échelle Au : plus la note Au est élevée, et plus sont faibles les gains qu’apporte chaque séance d’oreille électronique sur le test d’écoute.

Une critique méthodologique que l’on pourrait apporter à ce travail est le fait que plusieurs lignes sont présentes pour chaque sujet, ce qui pourrait biaiser les résultats. En effet, les sujets ayant reçu plus de séances que les autres ne sont pas forcément représentatifs de l’ensemble de la population. Or, ayant reçu plus de fois le test d’écoute, ils ont plus de lignes que les autres sujets, et ils pèsent d’autant plus lourd dans les calculs. Après discussion avec Mr Jean-René Mathieu, professeur de statistiques à l’Université Paul Sabatier à Toulouse, et spécialiste des modèles linéaires, une solution couramment admise consiste à calculer les moyennes des valeurs obtenues sur l’ensemble des lignes d’un sujet, puis à opérer une régression linéaire sur ces moyennes en pondérant la régression par le nombre de lignes. Cette fonctionnalité est prise en charge par le logiciel SPSS et nous l’avons donc mise en œuvre.

Effectivement, les résultats obtenus avec cette méthode sont moins marqués que précédemment, ce qui montre bien que les résultats précédents étaient légèrement biaisés.. Néanmoins, comme il apparaît dans le tableau suivant, ils restent tout à fait acceptables puisqu’une seule valeur dépasse très légèrement le seuil de p = .05, à savoir l’audition osseuse à 250 Hz où p = .0555.

Tableau 6 : Pentes de régression (pondérées), et seuils de signification
de l’échelle Au sur les gains apportés par la cure d’oreille électronique.

La méthodologie de constitution de l’échelle a été assez rigoureuse : l’ensemble de l’échelle Au, y compris  les paramètres de normalisation (moyenne et écart type) ont été établis à partir du seul fichier de calcul, c’est à dire à partir de la partie du fichier retenue pour l’élaboration de l’échelle (n = 313), sans tenir compte du fichier de vérification, c’est à dire de la partir du fichier global destinée à tester la validité de l’échelle obtenue. Par ailleurs toutes les données, que ce soit pour le calcul ou la vérification, ont été recueillies avant la constitution de l’échelle.

Les régressions de vérification ont été calculée sur la partie du fichier qui n’a pas servi à constituer l’échelle. Elles constituent donc bien un test de la capacité prédictive de l’échelle sur de nouveaux cas. De plus, seules les données recueillies au moment du premier test audiométrique ont été utilisées pour constituer l’échelle. Ainsi, l’échelle Au est réellement un outil diagnostique et pronostique : elle se calcule à partir de données recueillies avant l’application de la cure d’oreille électronique et permet d’obtenir une idée des gains qu’il est raisonnable d’espérer au moyen de la cure d’oreille électronique.

suite du mémoire

plan du mémoire